
科目: 来源:2012届江西省新余市中考模拟考试数学试卷(带解析) 题型:解答题
已知抛物线
【小题1】若抛物线经过原点,求m的值及顶点坐标,并判断抛物线顶点是否在第三象限的平分线所在的直线上;
【小题2】是否无论m取任何实数值,抛物线顶点一定不在第四象限?说明理由;当实数m变化时,列出抛物线顶点的纵、横坐标之间的函数关系式,并求出该函数的最小函数值.
查看答案和解析>>
科目: 来源:2012届江西省新余市中考模拟考试数学试卷(带解析) 题型:解答题
某超市经销甲、乙两种商品. 现有如下信息:
请根据以上信息,解答下列问题:
【小题1】甲、乙两种商品的进货单价各多少元?
【小题2】该超市平均每天卖出甲商品50件和乙商品20件.经调查发现,甲、乙两种商品零售单价分别每降0.2元,这两种商品每天可各多销售10件.为了使每天获取更大的利润,超市决定把甲、乙两种商品的零售单价都下降m元.设总利润为n元,请用含m的式子表示超市每天销售甲、乙两种商品获取的总利润n,在不考虑其他因素的条件下,当m定为多少时,才能使超市每天销售甲、乙两种商品获取的总利润最大?每天的最大利润是多少?
查看答案和解析>>
科目: 来源:2012届浙江宁波初三毕业考试数学试卷(带解析) 题型:解答题
如图,∠C=90º,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC于点E.F为射线CB上一点,使得∠CEF=∠ABC.设点P运动的时间为x秒.
【小题1】用含有x的代数式表示CE的长
【小题2】求点F与点B重合时x的值
【小题3】当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式
查看答案和解析>>
科目: 来源:2012届浙江宁波初三毕业考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系 中,抛物线
中,抛物线 与
与 轴交于点
轴交于点 ,与
,与 轴交于
轴交于 两点,直线
两点,直线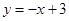 恰好经过
恰好经过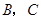 两点.
两点.
【小题1】求出抛物线 的解析式,并写出抛物线的对称轴;
的解析式,并写出抛物线的对称轴;
【小题2】点 在抛物线的对称轴上,抛物线顶点为D若
在抛物线的对称轴上,抛物线顶点为D若 ,求点
,求点 的坐标.
的坐标.
查看答案和解析>>
科目: 来源:2012届四川乐山市中区中考模拟数学试卷(带解析) 题型:解答题
如图,抛物线y=ax2+bx+c与x轴交于A(x1,0)、B(x2,0)两点,与y轴交于C点,对称轴与抛物线相交于点P,与直线BC相交于点M,连接PB.已知x1、x2
恰是方程 的两根,且sin∠OBC=
的两根,且sin∠OBC= .
.
【小题1】求该抛物线的解析式;
【小题2】抛物线上是否存在一点Q,使△QMB与△PMB的面积相等,若存在,求点Q的坐标;若不存在,说明理由
【小题3】在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相等,若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2012届山东省章丘市六中片区九年级学业水平考试数学卷(带解析) 题型:解答题
如图抛物线过坐标原点O和x轴上另一点E,顶点M为 (2,4);矩形ABCD顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
【小题1】求该抛物线所对应的函数关系式;
【小题2】将矩形ABCD以每秒1个单位长度的速从图示位置沿x轴正方向匀速平行移动,同时一动点P也以相同速度从点A出发向B匀速移动,设它们运动时间为t秒(0≤t≤3),直线AB与该抛物线交点为N
①当t= 时,判断点P是否在直线ME上,说明理由;
时,判断点P是否在直线ME上,说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?说明理由.
查看答案和解析>>
科目: 来源:2012届山东济南辛寨乡辛锐中学九年级下学业水平模拟考试数学卷(带解析) 题型:解答题
如图所示,已知在直角梯形 中,
中, 轴于点
轴于点 .动点
.动点 从
从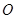 点出发,沿
点出发,沿 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过 点作
点作 垂直于直线
垂直于直线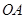 ,垂足为
,垂足为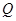 .设
.设 点移动的时间为
点移动的时间为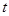 秒(
秒(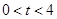 ),
),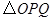 与直角梯形
与直角梯形 重叠部分的面积为
重叠部分的面积为 .
.
【小题1】求经过 三点的抛物线解析式;
三点的抛物线解析式;
【小题2】将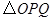 绕着点
绕着点 顺时针旋转
顺时针旋转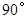 ,是否存在
,是否存在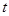 ,使得
,使得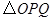 的顶点
的顶点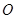 或
或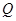 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出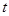 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【小题3】求 与
与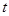 的函数关系式.
的函数关系式.
查看答案和解析>>
科目: 来源:2012届四川乐山沙湾区九年级毕业调研考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,抛物线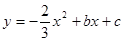 经过
经过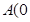 ,
,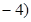 、
、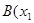 ,
,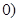 、
、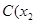 ,
,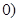 ,且
,且 .
.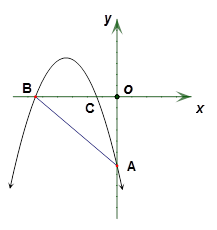
【小题1】求抛物线的解析式
【小题2】在抛物线上是否存在一点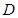 ,使得
,使得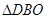 是以
是以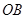 为底边的等腰三角形?若存在,求出点
为底边的等腰三角形?若存在,求出点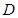 的坐标,并判断这个等腰三角形是否为等腰直角三角形?若不存在,请说明理由;
的坐标,并判断这个等腰三角形是否为等腰直角三角形?若不存在,请说明理由;
【小题3】连接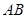 ,
,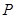 为线段
为线段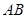 上的一个动点(点
上的一个动点(点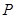 与
与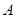 、
、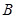 不重合),过
不重合),过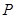 作
作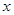 轴的垂线与这个二次函数的图象交于点
轴的垂线与这个二次函数的图象交于点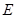 ,设线段
,设线段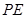 的长为
的长为 ,点
,点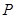 的横坐标为
的横坐标为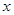 ,求
,求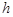 与
与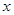 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量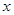 的取值范围
的取值范围
查看答案和解析>>
科目: 来源:2012届江西省南昌市九年级下学期第二次联考数学试卷(带解析) 题型:解答题
如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线折叠(点M在边AB上),使点B落在边AD上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P。
【小题1】①当点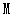 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点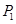 、
、 ,则
,则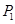 ( , )、
( , )、 ( , );②当∠OMN=60°时,对应的点P是点
( , );②当∠OMN=60°时,对应的点P是点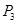 ,求
,求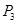 的坐标;
的坐标;
【小题2】若抛物线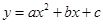 ,是经过(1)中的点
,是经过(1)中的点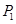 、
、 、
、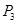 ,试求a、b、c的值;
,试求a、b、c的值;
【小题3】在一般情况下,设P点坐标是(x,y),那么y与x之间函数关系式还会与(2)中函数关系相同吗(不考虑x的取值范围)?请你利用有关几何性质(即不再用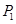 、
、 、
、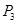 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.
查看答案和解析>>
科目: 来源:2011-2012学年江苏省无锡市崇安区九年级下学期期中考试数学卷(带解析) 题型:解答题
如图,在平面直角坐标系中,已知点A(0,1)、B(3,5),以AB为边作如图所示的正方形ABCD,顶点在坐标原点的抛物线恰好经过点D,P为抛物线上的一动点.
(1)直接写出点D的坐标;
(2)求抛物线的解析式;
(3)求点P到点A的距离与点P到x轴的距离之差;
(4)当点P位于何处时,△APB的周长有最小值,
并求出△APB的周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com