
科目: 来源:2012届北京石景山区初三第一模拟数学试卷(带解析) 题型:解答题
已知:关于 的方程
的方程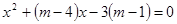 有两个不相等的实数根.
有两个不相等的实数根.
【小题1】求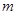 的取值范围;
的取值范围;
【小题2】抛物线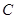 :
: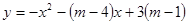 与
与 轴交于
轴交于 、
、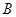 两点.若
两点.若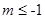 且直线
且直线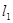 :
: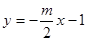 经过点
经过点 ,求抛物线
,求抛物线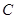 的函数解析式;
的函数解析式;
【小题3】在(2)的条件下,直线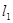 :
: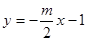 绕着点
绕着点 旋转得到直线
旋转得到直线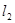 :
: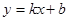 ,设直线
,设直线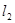 与
与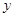 轴交于点
轴交于点 ,与抛物线
,与抛物线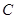 交于点
交于点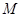 (
(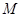 不与点
不与点 重合),当
重合),当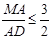 时,求
时,求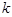 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2012届江苏无锡南长区九年级一模考试数学卷(带解析) 题型:解答题
如图,在平面直角坐标系xOy中,点B的坐标为(0,2),点D在x轴的负半
轴上,∠ODB=30°,OE为△BOD的中线,过B、E两点的抛物线y=ax2-x+c与x轴相交于A、F两点(A在F的右侧).
【小题1】求抛物线的解析式;
【小题2】点P是上述抛物线上一动点,若由点D、O、E、P构成四边形为梯形,则这样的点P有几个?试求出其中两个点P的坐标;
【小题3】等边△OMN的顶点M、N在线段AE上,求AE及AM的长.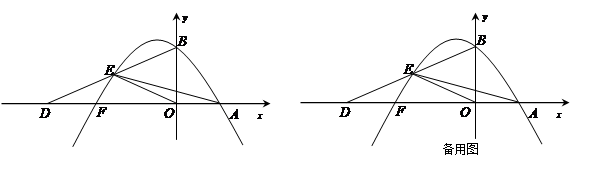
查看答案和解析>>
科目: 来源:2012届四川省沐川县初三二调考试数学卷(带解析) 题型:解答题
如图,已知抛物线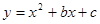 经过A(1,0),B(0,2)两点,顶点为D.
经过A(1,0),B(0,2)两点,顶点为D.
【小题1】求抛物线的解析式;
【小题2】将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图像的函数关系式;
【小题3】设(2)中平移后,所得抛物线与y轴的交点为 ,顶点为
,顶点为 ,若点N在平移后的抛物线上,且满足△
,若点N在平移后的抛物线上,且满足△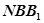 的面积是△
的面积是△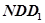 面积的2倍,求点N的坐标.
面积的2倍,求点N的坐标.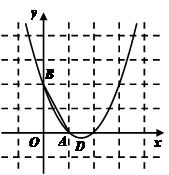
查看答案和解析>>
科目: 来源:2011-2012学年江苏江阴石庄中学九年级下学期期中考试数学卷(带解析) 题型:解答题
如图,抛物线 与
与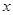 轴交于
轴交于 两点,于
两点,于 轴交于点
轴交于点 ,
,
(1)求出抛物线的解析式以及 ;
;
(2)在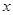 轴下方的抛物线上是否存在一点
轴下方的抛物线上是否存在一点 ,使四边形
,使四边形 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011-2012学年江苏泰州市九年级5月适应性考试数学卷(带解析) 题型:解答题
如图,抛物线 经过点A
经过点A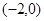 、B
、B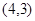 两点,且当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,经过点C
两点,且当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,经过点C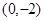 的直线
的直线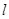 与x轴平行.
与x轴平行.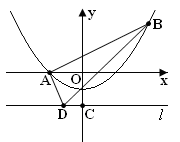
(1)求这条抛物线的解析式;
(2)若D是直线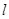 上的一个动点,求使△DAB的周长最小时点D的坐标;
上的一个动点,求使△DAB的周长最小时点D的坐标;
(3)以这条抛物线上的任意一点P为圆心,PO的长为半径作⊙P,试判断⊙P与直线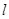 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目: 来源:2011-2012学年江苏省无锡南长区九年级一模数学卷(带解析) 题型:解答题
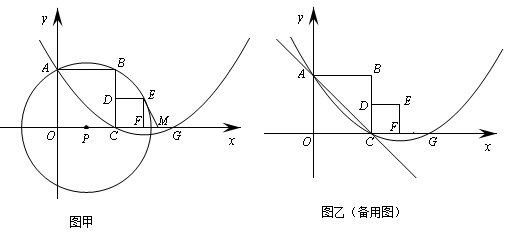
如图甲,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为 轴、
轴、 轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在
轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在 轴上),抛物线
轴上),抛物线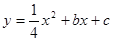 经过A、C两点,与
经过A、C两点,与 轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
(1)求B点坐标;
(2)求证:ME是⊙P的切线;
(3)设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,①求△ACQ周长的最小值;②若FQ= ,△ACQ的面积 S△ACQ=
,△ACQ的面积 S△ACQ=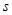 ,直接写出
,直接写出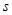 与
与 之间的函数关系式.?
之间的函数关系式.?
 |
查看答案和解析>>
科目: 来源:2011-2012学年江苏省无锡锡山区九年级下学期期中考试数学卷(带解析) 题型:解答题
如图,抛物线y=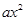 +bx+c的顶点为C(0,-
+bx+c的顶点为C(0,-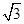 ),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒
),与x轴交于点A、B,连接AC、BC,得等边△ABC. T点从B点出发,以每秒1个单位的速度向点A运动,同时点S从点C出发,以每秒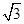 个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.
个单位的速度向y轴负方向运动,TS交射线BC于点D,当点T到达A点时,点S停止运动. 设运动时间为t秒.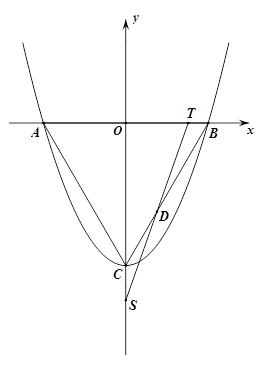
(1)求二次函数的解析式;
(2)设△TSC的面积为S,求S关于t的函数解析式;
(3)以点T为圆心,TB为半径的圆与射线BC交于点E,试说明:在点T运动的过程中,线段ED的长是一定值,并求出该定值.
查看答案和解析>>
科目: 来源:2011—2012学年江苏无锡育才中学第二学期第一次模拟考试数学卷(带解析) 题型:解答题
已知抛物线C1与x轴的一个交点为交于(-4,0),对称轴为直线x=-1.5,
并过点(-1,6)
【小题1】求抛物线C1的解析式;
【小题2】求出与抛物线C1关于原点对称的抛物线C2的解析式,并在C1所在的平面直角坐标系中画出C2的图像;
【小题3】在(2)的条件下,抛物线C1与抛物线C2与相交于A,B两点(点A在点B的左侧).
①求出点A和点B的坐标;
②点P在抛物线 上,且位于点A和点B之间;点Q在抛物线
上,且位于点A和点B之间;点Q在抛物线 上,也位于点A和点B之间.当PQ∥
上,也位于点A和点B之间.当PQ∥ 轴时,求PQ长度的最大值.
轴时,求PQ长度的最大值.
查看答案和解析>>
科目: 来源:2012届山东省德州市九年级中考模拟考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系 中,半径为1的圆的圆心
中,半径为1的圆的圆心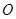 在坐标原点,且与两坐标轴分别交于
在坐标原点,且与两坐标轴分别交于 四点.抛物线
四点.抛物线 与
与 轴交于点
轴交于点 ,与直线
,与直线 交于点
交于点 ,且
,且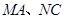 分别与圆
分别与圆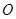 相切于点
相切于点 和点
和点 .
.
【小题1】求抛物线的解析式;
【小题2】抛物线的对称轴交 轴于点
轴于点 ,连结
,连结 ,并延长
,并延长 交圆
交圆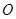 于
于 ,求
,求 的长.
的长.
【小题3】过点 作圆
作圆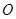 的切线交
的切线交 的延长线于点
的延长线于点 ,判断点
,判断点 是否在抛物线上,说明理由.
是否在抛物线上,说明理由.
查看答案和解析>>
科目: 来源:2012届江西省新余市中考模拟考试数学试卷(带解析) 题型:解答题
已知:如图(1),△OAB是边长为2的等边三角形,0A在x轴上,点B在第一象限内;△OCA是一个等腰三角形,OC=AC,顶点C在第四象限,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
【小题1】求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系,并写出自变量t的取值范围;
【小题2】在OA上(点O、A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
【小题3】如图(2),现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com