
科目: 来源:2012届江苏泰兴济川中学九年级中考一模数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,O是坐标原点,直线y =" 3x" + 9与x轴、y轴分别交于A、C两点,抛物线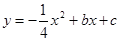 经过A、C两点,与x轴的另一个交点为点B,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动,动点N从点C出发沿CA
经过A、C两点,与x轴的另一个交点为点B,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动,动点N从点C出发沿CA
以每秒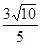 个单位长度的速度向点A运动,点P、Q、N同时出发、同时停止,设
个单位长度的速度向点A运动,点P、Q、N同时出发、同时停止,设
运动时间为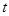 (0<
(0<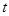 <5)秒.
<5)秒.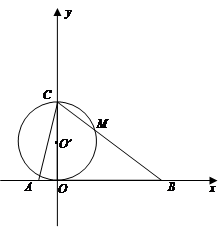
【小题1】求抛物线的解析式;
【小题2】判断△ABC的形状;
【小题3】以OC为直径的⊙O′与BC交于点M,求当t为何值时,PM与⊙O′相切?请说明理由;
【小题4】在点P、Q、N运动的过程中,是否存在△NCQ为直角三角形的情形,若存在,求出相应的t值;若不存在,请说明理由.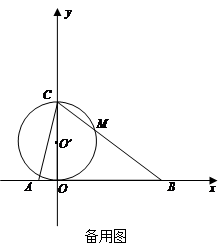
查看答案和解析>>
科目: 来源:2012届江苏泰兴济川中学九年级中考一模数学试卷(带解析) 题型:解答题
已知一次函数y1 = 2x和二次函数y2 = x2 + 1。
【小题1】求证:函数y1、y2的图像都经过同一个定点;
【小题2】求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2总成立;
【小题3】是否存在抛物线y3 = ax2 + bx + c,其图象经过点(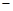 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
查看答案和解析>>
科目: 来源:2012届江苏泰兴济川中学九年级中考一模数学试卷(带解析) 题型:解答题
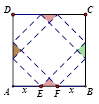
一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得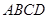 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE =" FB" = xcm。若广告商要求包装盒侧面积S(cm
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE =" FB" = xcm。若广告商要求包装盒侧面积S(cm )大,试问x应取的值为 cm.
)大,试问x应取的值为 cm.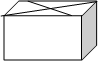
查看答案和解析>>
科目: 来源:2012届江苏苏州九年级中考模拟数学试卷(带解析) 题型:解答题
如图,抛物线y=ax2+bx+c的顶点为P,对称轴直线x=1与x轴交于点D,抛物线与x轴交于A、B两点,与y轴交于点C,其中A(-1,0)、C(0,3).
【小题1】求此抛物线的解析式
【小题2】点E在线段BC上,若△DEB为等腰三角形,求点E的坐标
【小题3】点F、Q都在该抛物线上,若点C与点F关于直线x=1成轴对称,连结BF、BQ,如果∠FBQ=45°,求点Q的坐标;
【小题4】将△BOC绕着它的顶点B顺时针在第一象限内旋转,旋转后的图形为△BO'C',BO'与BP重合时,则△BO'C'不在BP上的顶点C'的坐标为 ▲ (直接写出答案).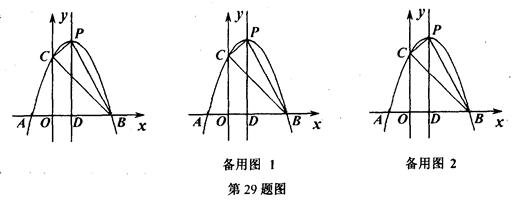
查看答案和解析>>
科目: 来源:2012届湖北省南漳县中考模拟数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A.B两点,开口向下的抛物线经过点A,B,且其顶点P在⊙C上.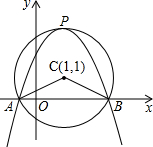
【小题1】求∠ACB的大小
【小题2】写出A,B两点的坐标
【小题3】由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3),求出抛物线的解析式;
【小题4】在该抛物线上是否存在一点D点,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届湖北保康中考模拟数学试卷(带解析) 题型:解答题
如图,已知抛物线y=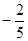 x2+
x2+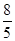 x+2交x轴于A、B两点(点A在点B的左侧),与y轴交于点C.
x+2交x轴于A、B两点(点A在点B的左侧),与y轴交于点C.
【小题1】求点A、B、C的坐标.
【小题2】若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积
【小题3】连接AC,在x轴上是否存在点P使△ACP为等腰三角形,若存在,请求出点P的坐标;若不存在请说明理由
查看答案和解析>>
科目: 来源:2012届浙江省温州地区初三适应性考试数学卷(带解析) 题型:解答题
如图,抛物线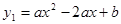 的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB =" 2OC=" 3.
的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB =" 2OC=" 3.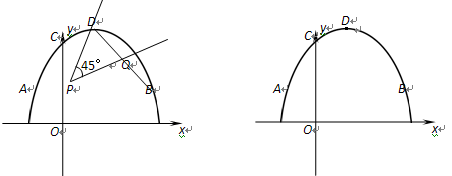
(1)求a,b的值;
(2)将45°角的顶点P在线段OB上滑动(不与点B重合),该角的一边过点D,另一边与BD交于点Q,设P(x,0),y2= DQ,试求出y2关于x的函数关系式;
DQ,试求出y2关于x的函数关系式;
(3)在同一平面直角坐标系中,两条直线x = m,x = m+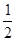 分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为
分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为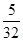 ?若能,求出m的值;若不能,请说明理由.
?若能,求出m的值;若不能,请说明理由.
查看答案和解析>>
科目: 来源:2011-2012学年北京市朝阳区中考一模数学卷(带解析) 题型:解答题
在平面直角坐标系xOy中,抛物线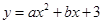 经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
(1)求此抛物线的解析式;
(2)点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
(3)设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM ?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2011-2012学年北京市朝阳区中考一模数学卷(带解析) 题型:解答题
根据对北京市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的
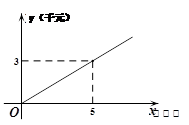
甲种蔬菜的销售利润y1(千元)与进货量x(吨)之间的函数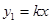 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数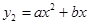 的图象如图②所示.
的图象如图②所示.
(1)分别求出y1、y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种蔬菜共10吨,设乙种蔬菜的进货量为t吨,写出这两种蔬菜所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种蔬菜各进多少吨时获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
科目: 来源:2012届北京石景山区初三第一模拟数学试卷(带解析) 题型:解答题
已知二次函数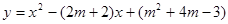 中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
【小题1】求这个二次函数的解析式;
【小题2】点C是抛物线与 轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
【小题3】在(2)的情况下,求四边形ACQD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com