
科目: 来源:2012届广东省汕头市潮南区中考模拟考试数学卷(带解析) 题型:解答题
如图,已知抛物线y=x -ax+a
-ax+a -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.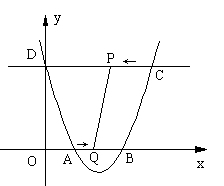
(1)求a的值;(2)当四边形ODPQ为矩形时,求这个矩形的面积;(3)当四边形PQBC的面积等于14时,求t的值.(4)当t为何值时,△PBQ是等腰三角形?(直接写出答案)
查看答案和解析>>
科目: 来源:2012届广东省汕头市潮南区中考模拟考试数学卷(带解析) 题型:解答题
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目: 来源:2012届浙江十校九年级5月模拟数学试卷(带解析) 题型:解答题
如图,已知直线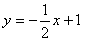 交坐标轴于
交坐标轴于 两点,以线段
两点,以线段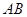 为边向上作正方形
为边向上作正方形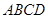 ,过点
,过点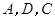 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为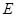 .
.
【小题1】请直接写出点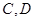 的坐标
的坐标
【小题2】求抛物线的解析式
【小题3】若正方形以每秒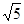 个单位长度的速度沿射线
个单位长度的速度沿射线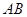 下滑,直至顶点
下滑,直至顶点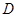 落在
落在 轴上时停止.设正方形落在
轴上时停止.设正方形落在 轴下方部分的面积为
轴下方部分的面积为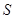 ,求
,求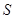 关于滑行时间
关于滑行时间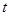 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量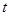 的取值范围;
的取值范围;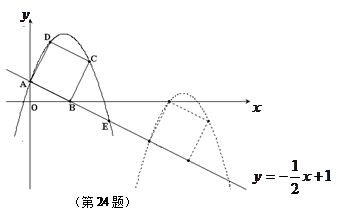
【小题4】在(3)的条件下,抛物线与正方形一起平移,当D落在x轴上时,抛物线与正方形同时停止,求抛物线上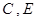 两点间的抛物线弧所扫过的面积.
两点间的抛物线弧所扫过的面积.
查看答案和解析>>
科目: 来源:2012届广东汕头澄海区中考模拟数学试卷(带解析) 题型:解答题
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线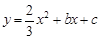 经过B点,且顶点在直线
经过B点,且顶点在直线 上.
上.
【小题1】求抛物线对应的函数关系式;
【小题2】若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由
【小题3】在(2)的条件下,连结BD,已知在对称轴上存在一点P,使得△PBD的周长最小.请求出点P的坐标.
【小题4】在(2)、(3)的条件下,若点M是线段OB上的一个动点(与点O、B不重合),过点M作MN∥BD交x轴于点N,连结PM、PN,设OM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在最大值?若存在,求出最大值并求此时M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届广东汕头龙湖区中考模拟数学试卷(带解析) 题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成△AC1D1和△BC2D2两个三角形(如图2所示).将纸片△AC1D1沿直线D2B(AB)方向平移(点A,D1,D2,B始终在同一直线上),当点D1与点B重合时,停止平移.在平移的过程中,C1D1与BC2交于点E,AC1与C2D2、BC2分别交于点F、P.
【小题1】当△AC1D1平移到如图3所示位置时,猜想D1E与D2F的数量关系,并说明理由
【小题2】设平移距离D2D1为x,△AC1D1和△BC2D2重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
【小题3】对于(2)中的结论是否存在这样的x,使得重复部分面积等于原△ABC纸片面积的 ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.
图1 图2 图3
查看答案和解析>>
科目: 来源:2012届广东汕头龙湖区中考模拟数学试卷(带解析) 题型:解答题
如图,已知二次函数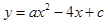 的图像经过点A和点B.
的图像经过点A和点B.
【小题1】求该二次函数的表达式
【小题2】写出该抛物线的对称轴及顶点坐标;
【小题3】点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求P、Q两点的坐标及点Q 到x轴的距离. 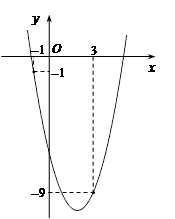
查看答案和解析>>
科目: 来源:2012届江苏常州武进区九年级5月调研测试数学试卷(带解析) 题型:解答题
如图,□ABCD中,AB=4,BC=3,∠BAD=120°,动点E在BC上(不与B
重合).作EF⊥AB于F,FE、DC的延长线交于点G.设BE=x,△DEF的面积为S.
【小题1】求S关于x的函数表达式,并写出x的取值范围
【小题2】当点E在何处时,S有最大值,最大值为多少?
查看答案和解析>>
科目: 来源:2012届浙江省椒江区九年级二模数学试卷(带解析) 题型:解答题
如图①,在平面直角坐标系中,等腰直角△AOB的斜边OB在x轴上,顶点A的坐标为(3,3),AD为斜边上的高.抛物线y=ax2+2x与直线y=x交于点O、C,点C的横坐标为6.点P在x轴的正半轴上,过点P作PE∥y轴,交射线OA于点E.设点P的横坐标为m,以A、B、D、E为顶点的四边形的面积为S.
【小题1】求OA所在直线的解析式.
【小题2】求a的值.
【小题3】当m≠3时,求S与m的函数关系式
【小题4】如图②,设直线PE交射线OC于点R,交抛物线于点Q.以RQ为一边,在RQ的右侧作矩形RQMN,其中RN=.直接写出矩形RQMN与△AOB重叠部分为轴对称图形时m的取值范围.
查看答案和解析>>
科目: 来源:2012届浙江宁波北仑区中考模拟数学试卷(带解析) 题型:解答题
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,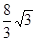 ).
).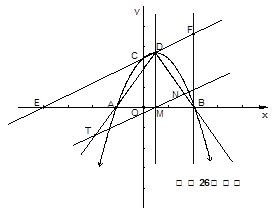
【小题1】求抛物线的解析式及其顶点D的坐标;
【小题2】设直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,在直线CD的上方,y轴及y轴的右侧的平面内找一点G,使以点G、F、C为顶点的三角形与△COE相似,请直接写出符合要求的点G的坐标;
【小题3】如图,抛物线的对称轴与x轴的交点M,过点M作一条直线交∠ADB于T,N两点,①当∠DNT=90°时,直接写出 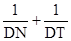 的值;
的值;
②当直线TN绕点M旋转时,
试说明: △DNT的面积S△DNT=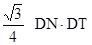 ;
;
并猜想 :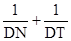 的值是否是定值?说明理由.
的值是否是定值?说明理由.
查看答案和解析>>
科目: 来源:2012届山东省临沂市中考模拟数学试卷(带解析) 题型:解答题
如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.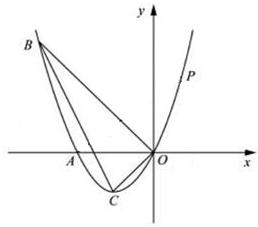
【小题1】求抛物线的解析式
【小题2】若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标
【小题3】P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com