
科目: 来源:2012届江苏宜兴和桥学区九年级5月模拟考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3,1)、C(-3,0)、O(0,0).将此矩形沿着过E(-,1)、
F(-,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′
【小题1】求折痕所在直线EF的解析式
【小题2】一抛物线经过B、E、B′三点,求此二次函数解析式;
【小题3】能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由.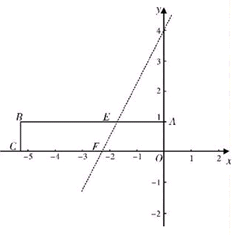
查看答案和解析>>
科目: 来源:2012届江苏无锡滨湖中学九年级中考二模数学试卷(带解析) 题型:解答题
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),
与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
【小题1】求抛物线的函数表达式
【小题2】求直线BC的函数表达式
【小题3】点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ=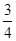 AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标。
查看答案和解析>>
科目: 来源:2012届江苏无锡滨湖中学九年级中考二模数学试卷(带解析) 题型:解答题
某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润(万元)与投资金额 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: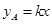 ;如果单独投资B种产品,则所获利润(万元)与投资金额
;如果单独投资B种产品,则所获利润(万元)与投资金额 (万元)之间满足二次函数关系:
(万元)之间满足二次函数关系: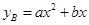 .根据公司信息部的报告,
.根据公司信息部的报告,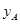 ,
,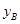 (万元)与投资金额
(万元)与投资金额 (万元)的部分对应值如下表所示
(万元)的部分对应值如下表所示
【小题1】填空: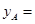 ▲ ;
▲ ;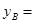 ▲ ;
▲ ;
【小题2】如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为w(万元),试写出w与某种产品的投资金额n之间的函数关系式;
【小题3】请你设计一个在⑵中能获得最大利润的投资方案
查看答案和解析>>
科目: 来源:2011-2012学年浙江金华五中九年级阶段性测试数学试卷(带解析) 题型:解答题
如图,抛物线y=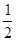 x2+bx-2与x轴交于A、B两点,与y 轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y 轴交于C点,且A(一1,0).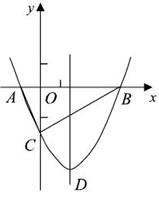
【小题1】求抛物线的解析式及顶点D的坐标;
【小题2】若将上述抛物线先向下平移3个单位,再向右平移2个单位,
请直接写出平移后的抛物线的解析式.
查看答案和解析>>
科目: 来源:2012届四川仁寿联谊学校中考模拟数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,抛物线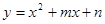 经过A(3,0),B(0,-3)两点,点P是直线AB上一动点,过点P作
经过A(3,0),B(0,-3)两点,点P是直线AB上一动点,过点P作 轴的垂线交抛物线于点M,设点P的横坐标为t,
轴的垂线交抛物线于点M,设点P的横坐标为t,
【小题1】分别求直线AB和这条抛物线的解析式(4分)
【小题2】若点P在第四象限,连结BM、AM,当线段PM最长时,求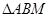 的面积。(4分)
的面积。(4分)
③ 【小题3】是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由(3分)。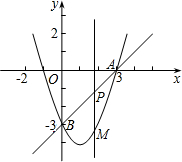
查看答案和解析>>
科目: 来源:2012届湖北黄石九年级5月联考数学试卷(带解析) 题型:解答题
如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2-2x-8=0的两个根.
【小题1】求这条抛物线的解析式;
【小题2】点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
【小题3】探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形,若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届湖北黄石九年级5月联考数学试卷(带解析) 题型:解答题
连接上海市区到浦东国际机场的磁悬浮轨道全长约为 ,列车走完全程包含启动加速、匀速运行、制动减速三个阶段.已知磁悬浮列车从启动加速到稳定匀速动行共需
,列车走完全程包含启动加速、匀速运行、制动减速三个阶段.已知磁悬浮列车从启动加速到稳定匀速动行共需 秒,在这段时间内记录下下列数据:
秒,在这段时间内记录下下列数据:
时间 (秒) (秒) | 0 | 50 | 100 | 150 | 200 |
速度 (米/秒) (米/秒) | 0 | 30 | 60 | 90 | 120 |
路程 (米) (米) | 0 | 750 | 3000 | 6750 | 12000 |
 )速度
)速度 与时间
与时间 的函数关系、路程
的函数关系、路程 与时间
与时间 的函数关系
的函数关系 (米)与时间
(米)与时间 (秒)的函数关系式(不需要写出过程)
(秒)的函数关系式(不需要写出过程)查看答案和解析>>
科目: 来源:2012届浙江衢州地区中考试第二次模拟考试数学试卷(带解析) 题型:解答题
如图1,点C、B分别为抛物线C1:y1=x2+1,抛物线C2:y2=a2x2+b2x+c2的顶点.分别过点B、C作x轴的平行线,交抛物线C1、C2于点A、D,且AB=BD.
【小题1】求点A的坐标:
【小题2】如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=2x2+b1x+c1”.其他条件不变,求CD的长和a2的值;
【小题3】如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=4x2+b1x+c1”,其他条件不变,求b1+b2的值 2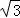 (直接写结果).
(直接写结果).
查看答案和解析>>
科目: 来源:2012届广东省汕头市濠江区中考模拟考试数学卷(带解析) 题型:解答题
如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(-2,0),B(-1, -3).
(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标;
(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P的坐标. 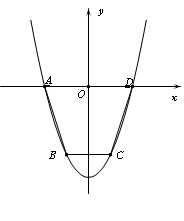
查看答案和解析>>
科目: 来源:2012届广东省汕头市濠江区中考模拟考试数学卷(带解析) 题型:解答题
若 是关于
是关于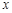 的一元二次方程
的一元二次方程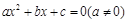 的两个根,则方程的两个根
的两个根,则方程的两个根 和系数
和系数 有如下关系:
有如下关系: . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数 的图象与x轴的两个交点为
的图象与x轴的两个交点为 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
请你参考以上定理和结论,解答下列问题:
设二次函数 的图象与x轴的两个交点为
的图象与x轴的两个交点为 ,抛物线的顶点为
,抛物线的顶点为 ,显然
,显然 为等腰三角形.
为等腰三角形.
(1)当 为等腰直角三角形时,求
为等腰直角三角形时,求
(2)当 为等边三角形时,求
为等边三角形时,求
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com