
科目: 来源:2012届福建建宁九年级学业质量检测考试数学试卷(带解析) 题型:解答题
如图:在直角坐标系中,以点A(3,0)为圆心,以5为半径的圆与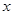 轴相交于B、C两点,与
轴相交于B、C两点,与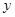 轴相交于D、E两点.
轴相交于D、E两点.
【小题1】若抛物线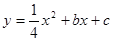 经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?(5分)
经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?(5分)
【小题2】过点E的直线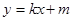 交
交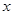 轴于F(
轴于F(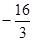 ,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;(5分)
,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;(5分)
【小题3】探索:是否能在(1)中的抛物线上找到一点Q,使直线BQ与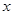 轴正方向所夹锐角的正切值等于
轴正方向所夹锐角的正切值等于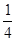 ?,若能,请直接写出Q点坐标;若不能,请说明理由. (4分)
?,若能,请直接写出Q点坐标;若不能,请说明理由. (4分)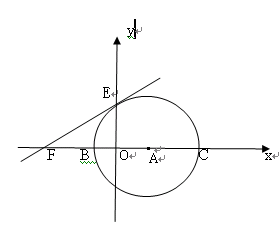
查看答案和解析>>
科目: 来源:2012届福建省泰宁县九年级学业质量检测考试数学试卷(带解析) 题型:解答题
如图,已知抛物线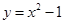 与
与 轴交于A、B两点,与
轴交于A、B两点,与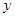 轴交于点C.
轴交于点C.
【小题1】求A、B、C三点的坐标.
【小题2】过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
【小题3】在 轴上方的抛物线上是否存在一点M,过M作MG
轴上方的抛物线上是否存在一点M,过M作MG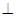
 轴于点G,使以A、M、G三点为顶点的三角形与
轴于点G,使以A、M、G三点为顶点的三角形与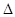 PCA相似.若存在,直接写出所有满足要求的M点的坐标;否则,请说明理由.
PCA相似.若存在,直接写出所有满足要求的M点的坐标;否则,请说明理由.
查看答案和解析>>
科目: 来源:2012届福建省宁化县九年级学业质量检测考试数学试卷(带解析) 题型:解答题
如图1,在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a>0)的图像顶点为D,与y轴交于点C,与x轴交于点A、B,点A在原点的左侧,点B的坐标为(3,0),OB=OC,tan∠ACO=.
【小题1】求这个二次函数的解析式;
【小题2】若平行于x轴的直线与该抛物线交于点M、N,且以MN为直径的圆与x轴相切,求该圆的半径长度;Com]
【小题3】如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,△AGP的面积最大?求此时点P的坐标和△AGP的最大面积.

查看答案和解析>>
科目: 来源:2012届江苏省无锡市惠山区九年级5月模拟考试数学试卷(带解析) 题型:解答题
如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.
【小题1】求点E、F的坐标(用含m的式子表示);
【小题2】连接OA,若△OAF是等腰三角形,求m的值;
【小题3】如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,
若∠OAM=90°,求a、h、m的值. 
(1) (2)
查看答案和解析>>
科目: 来源:2012届湖北武汉部分学校九年级5月供题调研数学试卷(带解析) 题型:解答题
如图,已知正方形ABCD,点P为射线BA上的一点(不和点A,B重合),过P作PE⊥CP,且CP=PE.过E作EF∥CD交射线BD于F.
【小题1】若CB=6,PB=2,则EF= ;DF= ;
【小题2】请探究BF,DG和CD这三条线段之间的数量关系,写出你的结论并证明;
【小题3】如图2,点P在线段BA的延长线上,当tan∠BPC= 时,四边形EFCD与四边形PEFC的面积之比为 .
.
查看答案和解析>>
科目: 来源:2012届湖北武汉部分学校九年级5月供题调研数学试卷(带解析) 题型:解答题
如图1,已知抛物线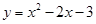 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.
【小题1】求A、B、C三点的坐标
【小题2】点D为射线CB上的一动点(点D、B不重合),过点B作x轴的垂线BE与以点D为顶点的抛物线y=(x-t)2+h相交于点E,从△ADE和△ADB中任选一个三角形,求出当其面积等于△ABE的面积时的t的值;(友情提示:1、只选取一个三角形求解即可;2、若对两个三角形都作了解答,只按第一个解答给分.)
【小题3】如图2,若点P是直线 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
查看答案和解析>>
科目: 来源:2012届湖北武汉部分学校九年级5月供题调研数学试卷(带解析) 题型:解答题
某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面 米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
【小题1】求这条抛物线的解析式;
【小题2】在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中完成规定的翻腾动作并调整好入水姿势时,距池边的水平距离为 米,问此次跳水会不会失误?并通过计算说明理由.
米,问此次跳水会不会失误?并通过计算说明理由.
查看答案和解析>>
科目: 来源:2012届江苏江阴南菁中学九年级中考适应性训练数学试卷(带解析) 题型:解答题
已知:在△ABC中,AB=AC,∠B=30°,BC=6,动点P以每秒 个单位从点B出发沿线段BA、AC运动,过点P作边长为3的等边△FDE,使得点D在线段BC上,点E在线段DC上.
个单位从点B出发沿线段BA、AC运动,过点P作边长为3的等边△FDE,使得点D在线段BC上,点E在线段DC上.
【小题1】如图(1),当EF经过点A时,动点P运动时间t为多少?
【小题2】设点P运动t秒时,△ABC与△DEF重叠部分面积为S,求S关于t的函数关系式
【小题3】如图(2),在点P的运动过程中,是否存在时间t,使得以点P为圆心,AP为半径的圆与△FDE三边所在的直线相切.如果存在,请直接写出t的值;如不存在,说明理由.

查看答案和解析>>
科目: 来源:2012届江苏江阴南菁中学九年级中考适应性训练数学试卷(带解析) 题型:解答题
已知:如图,二次函数y=a(x+1)2-4的图象与x轴分别交于A、B两点,与y轴交于点D,点C是二次函数y=a(x+1)2-4的图象的顶点,CD=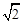 .
.
【小题1】求a的值
【小题2】点M在二次函数y=a(x+1)2-4图象的对称轴上,且∠AMC=∠BDO,求点M的坐标.
【小题3】将二次函数y=a(x+1)2-4的图象向下平移k(k>0)个单位,平移后的图象与直线CD分别交于E、F两点(点F在点E左侧),设平移后的二次函数的图象的顶点为C1,与y轴的交点为D1,是否存在实数k,使得CF⊥FC1,若存在,求出k的值;若不存在,请说明理由.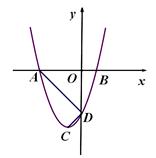
查看答案和解析>>
科目: 来源:2012届江苏宜兴和桥学区九年级5月模拟考试数学试卷(带解析) 题型:解答题
如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
【小题1】求证:△DHQ∽△ABC
【小题2】求y关于x的函数解析式并求y的最大值
【小题3】当x为何值时,△HDE为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com