
科目: 来源:2012届福建尤溪初中毕业学业质量检测数学试卷(带解析) 题型:解答题
如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.
【小题1】求b+c的值
【小题2】若点C在抛物线上,且四边形OABC是平行四边形,试求抛物线的解析式;
【小题3】在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标.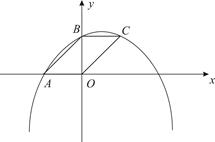
查看答案和解析>>
科目: 来源:2012届福建厦门外国语学校九年级中考模拟数学试卷(带解析) 题型:解答题
在平面直角坐标系xOy中,抛物线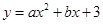 经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
【小题1】求此抛物线的解析式
【小题2】点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
【小题3】设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM ?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2012届河南省中招临考猜题(六)数学试卷(带解析) 题型:解答题
如图①,二次函数的抛物线的顶点坐标C,与x轴的交于A(1,0)、B(-3,0)两点,与y轴交于点D(0,3)
【小题1】求这个抛物线的解析式
【小题2】如图②,过点A的直线与抛物线交于点E,交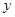 轴于点F,其中点E的横坐标为-2,若直线
轴于点F,其中点E的横坐标为-2,若直线 为抛物线的对称轴,点G为直线
为抛物线的对称轴,点G为直线 上的一动点,则
上的一动点,则 轴上是否存在一点H,使
轴上是否存在一点H,使 四点所围成的四边形周长最小,若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;
四点所围成的四边形周长最小,若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;
【小题3】如图③,连接AC交y轴于M,在x轴上是否存在点P,使以P、C、M为顶点的三角形与△AOM相似?若存在,求出点P的坐标;若不存在,请说明理由.
图① 图②
图③
查看答案和解析>>
科目: 来源:2012届辽宁省丹东七中九年级下学期第二次模拟考试数学卷(带解析) 题型:解答题
如图,在平面直角坐标系中,直线 与
与 轴交于点A,与y轴交于点C. 抛物线
轴交于点A,与y轴交于点C. 抛物线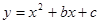 经过A、C两点,且与x轴交于另一点B(点B在点A右侧).
经过A、C两点,且与x轴交于另一点B(点B在点A右侧).
【小题1】求抛物线的解析式及点B坐标;
【小题2】若点M是线段BC上一动点,过点M的直线EF平行y轴交 轴于点F,交抛物线于点E.求ME长的最大值;
轴于点F,交抛物线于点E.求ME长的最大值;
【小题3】试探究当ME取最大值时,在抛物线x轴下方是否存在点P,使以M、F、B、P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目: 来源:2011届辽宁省丹东七中九年级中考一模数学试题(带解析) 题型:解答题
如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(-1,0),(5,0),(0,2)
【小题1】求过A、B、C三点的抛物线解析式.
【小题2】若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P运动的时间为t秒,(0≤t≤6)设△PBF的面积为S.
①求S与t的函数关系式.
②当t是多少时,△PBF的面积最大,最大面积是多少?
【小题3】点P在移动的过程中,△PBF能否成为直角三角形?若能,直接写出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源:2011届辽宁省丹东七中九年级中考一模数学试题(带解析) 题型:解答题
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
【小题1】设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
【小题2】如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
【小题3】根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目: 来源:2012届江苏镇江九年级5月中考模拟数学试卷(带解析) 题型:解答题
如图,将一把直角三角板的直角顶点放置于原点O,两直角边与抛物线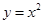 交于M、N两点,设M、N的横坐标分别为m、n(m﹥0,n﹤0);请解答下列问题:
交于M、N两点,设M、N的横坐标分别为m、n(m﹥0,n﹤0);请解答下列问题:
【小题1】当m=1时,n=__ ▲ ; 当m=2时,n=__ ▲ 试猜想m与n满足的关系,并证明你猜想的结论。
【小题2】连接M、N,若△OMN的面积为S,求S关于m的函数关系式。
【小题3】当三角板绕点O旋转到某一位置时,恰好使得∠MNO=30°,此时过M作MA⊥x轴,垂足为A,求出△OMA的面积
【小题4】当m=2时,抛物线上是否存在一点P使M、N、O、P四点构成梯形,若存在,直接写出所有满足条件的点P的坐标;若不存在,说明理由。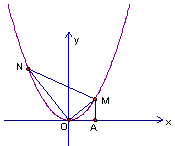
查看答案和解析>>
科目: 来源:2012届江苏镇江九年级5月中考模拟数学试卷(带解析) 题型:解答题
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量 y(件)与销售单价x (元)符合一次函数y=  ,
,
【小题1】若该商场获得利润为w 元,试写出利润w 与销售单价x 之间的关系式;销售单价x定为多少元时,商场可获得最大利润,最大利润是多少元?
【小题2】若该商场获得利润不低于500元,试确定销售单价的范围.
查看答案和解析>>
科目: 来源:2012届江苏镇江九年级第二次中考模拟数学试卷(带解析) 题型:解答题
在平面直角坐标系中,已知抛物线 与
与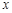 轴交于点
轴交于点 (-1,0)、
(-1,0)、 (3,0),与
(3,0),与 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
,顶点为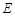 .
.
【小题1】求抛物线解析式及顶点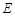 的坐标;
的坐标;
【小题2】如图,过点E作BC平行线,交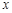 轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: .
轴于点F,在不添加线和字母情况下,图中面积相等的三角形有: .
【小题3】将抛物线向下平移,与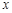 轴交于点M、N,与
轴交于点M、N,与 轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
轴的正半轴交于点P,顶点为Q.在四边形MNQP中满足S△NPQ = S△MNP,求此时直线PN的解析式
查看答案和解析>>
科目: 来源:2012届苏盐都郭猛中学九年级毕业班学情调研数学试卷(带解析) 题型:解答题
已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,3)三点,连接AB,过点B作BC∥ 轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动,动点E、F有一个点到达目的点即停止全部运动.设动点运动的时间为t(秒).
轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动,动点E、F有一个点到达目的点即停止全部运动.设动点运动的时间为t(秒).
【小题1】求抛物线的解析式
【小题2】记△EFA的面积为S,求S关于t的函数关系式,并求S的最大值;
【小题3】是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com