已知：抛物线y＝－x²＋2x＋m-2交y轴于点A（0，2m-7）．与直线
y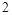＝x交于点B、C（B在右、C在左）．
【小题1】求抛物线的解析式
【小题2】设抛物线的顶点为E，在抛物线的对称轴上是否存在一点F，使得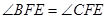，若存在，求出点F的坐标，若不存在，说明理由
【小题3】射线OC上有两个动点P、Q同时从原点出发，分别以每秒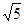个单位长度、每秒2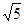个单位长度的速度沿射线OC运动，以PQ为斜边在直线BC的上方作直角三角形PMQ（直角边分别平行于坐标轴），设运动时间为t秒，若△PMQ与抛物线y＝－x²＋2x＋m-2有公共点，求t的取值范围．

如图，Rt△AOC中，∠ACO=90°，∠AOC=30°．将Rt△AOC绕OC中点E按顺时针方向旋转180°后得到Rt△BCO，BO、CO恰好分别在y轴、x轴上．再将Rt△BCO沿y轴对折得到Rt△BDO．取BC中点F，连接DF，交AB于点G，将△BDG沿DF对折得到△KDG．直线DK交AB于点H．

【小题1】填空：CE:ED=________,AB:AC=__________；
【小题2】若BH=，求直线BD解析式
【小题3】在（2）的条件下，一抛物线过点D、点E、点B，此抛物线位于直线BD上方有一动点Q,△BDQ的面积有无最大值？若有，请求出点Q的坐标；若无，请说明理由

某商场销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=－10x+500．
【小题1】设商场每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
【小题2】若物价部门规定，这种护眼台灯的销售单价不得高于32元，求该商场每月可获得最大利润．

如图，在平面直角坐标系中，已知二次函数的图像与轴交于点，与轴交于A、B两点，点B的坐标为
【小题1】 求二次函数的解析式及顶点D的坐标；
【小题2】 点M是第二象限内抛物线上的一动点，若直线OM把四边形ACDB分成面积为1:2的两部分，求出此时点的坐标；
【小题3】点P是第二象限内抛物线上的一动点，问：点P在何处时△的面积最大？最大面积是多少？并求出 此时点P的坐标.
                                     

已知关于的方程．
【小题1】若方程有两个不相等的实数根，求的取值范围；
【小题2】 若正整数满足，设二次函数的图象与轴交于两点，将此图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当直线与此图象恰好有三个公共点时，求出的值（只需要求出两个满足题意的k值即可）．

在平面直角坐标系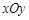中，抛物线经过A（－3,0）、B（4,0）两点，且与y轴交于点C，点D在x轴的负半轴上，且BD＝BC，有一动点P从点A出发，沿线段AB以每秒1个单位长度的速度向点B移动，同时另一个动点Q从点C出发，沿线段CA以某一速度向点A移动.

【小题1】求该抛物线的解析式；
【小题2】若经过t秒的移动，线段PQ被CD垂直平分，求此时t的值；
【小题3】该抛物线的对称轴上是否存在一点M，使MQ＋MA的值最小？若存在，求出点M的坐标；若不存在，请说明理由.

已知二次函数．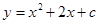
【小题1】当c＝－3时，求出该二次函数的图象与x轴的交点坐标；
【小题2】若－2＜x＜1时，该二次函数的图象与x轴有且只有一个交点，求c的取值范围．

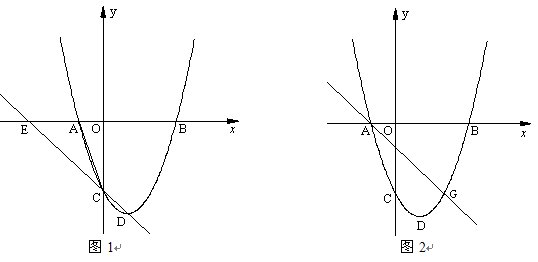
如图1，在平面直角坐标系中，二次函数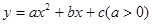的图象的顶点为D点，与y轴交于C点，与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），OB＝OC ，tan∠ACO＝．

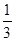（1）求这个二次函数的表达式；
（2）经过C、D两点的直线，与x轴交于点E，在该抛物线上是否存在这样的点F，使以点A、C、E、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由；
（3）若平行于x轴的直线与该抛物线交于M、N两点，且以MN为直径的圆与x轴相切，求该圆半径的长度；
（4）如图2，若点G（2，y）是该抛物线上一点，点P是直线AG下方的抛物线上一动点，当点P运动到什么位置时，△APG的面积最大？求出此时P点的坐标和△APG的最大面积.

如图，已知点A (0，4) 和点B (3，0)都在抛物线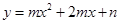上．

（1）求、n；
（2）向右平移上述抛物线，记平移后点A的对应点为D，点B的对应点为C，若四边形A BCD为菱形，求平移后抛物线的表达式；
（3）记平移后抛物线的对称轴与直线AC的交点为点E，试在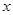轴上找点F，使得以点C、E、F为顶点的三角形与△    ABE相似。

如图,已知点A (-2,4) 和点B (1,0)都在抛物线y=mx²+2mx+n上．

（1）求m、n值；
（2）向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形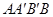为菱形,求平移后抛物线的表达式；
（3）试求出菱形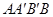的对称中心点M的坐标．