
科目: 来源:2012届河南三门峡实验中学一模数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线 y=" -" 4x点D.直线OD的解析式为
y=" -" 4x点D.直线OD的解析式为 ,点P(x,o)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.
,点P(x,o)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.
【小题1】直接写出点D的坐标及n的值
【小题2】判断抛物线的顶点是否在直线OM上?并说明理由
【小题3】设以M、E、H、N为顶点的四边形的面积为S.当x≠3[时,求S与x的函数关系式.
查看答案和解析>>
科目: 来源:2012届河南三门峡实验中学一模数学试卷(带解析) 题型:解答题
如图,把…张长10cm,宽8cm的矩形硬纸枥的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
【小题1】要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
【小题2】你感到折合而成的长方体盒子的侧面积(不含底面)会不会有最大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由
查看答案和解析>>
科目: 来源:2012届河北石家庄初中毕业班教学质量检测数学试卷(带解析) 题型:解答题
如图18-1所示,已知二次函数 与x轴分别交于点A(2,0)、
与x轴分别交于点A(2,0)、
B(4,0),与y轴交于点C(0,-8t)(t>0)
【小题1】求a、c的值及抛物线顶点D的坐标(用含t的代数式表示);
【小题2】如图18-1,连接AC,将△OAC沿直线AC翻折,若点O的对应点O′恰好落在该抛物线的对称轴上,求实数t的值;
【小题3】如图18-2,在正方形EFGH中,点E、F的坐标分别是(4,-4)、(4,-3),边HG位于边EF的右侧.若点P是边EF或边FG上的任意一点(不与E、F、G重合),请你说明以PA、PB、PC、PD的长度为边长不能构成平行四边形;
【小题4】将(3)中的正方形EFGH水平移动,若点P是正方形边FG或EH上任意一点,在水平移动过程中,是否存在点P,使以PA、PB、PC、PD的长度为边长构成平行四边形,其中PA、PB为对边.若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届北京门头沟中考二模数学试卷(带解析) 题型:解答题
如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为 ,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
【小题1】求出点C的坐标
【小题2】求S随t变化的函数关系式;
【小题3】当t为何值时,S有最大值?并求出这个最大值
查看答案和解析>>
科目: 来源:2012届北京门头沟中考二模数学试卷(带解析) 题型:解答题
已知抛物线y=ax2+x+2.
【小题1】当a=-1时,求此抛物线的顶点坐标和对称轴
【小题2】若代数式-x2+x+2的值为正整数,求x的值;
【小题3】若a是负数时,当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点M(m,0);当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点N(n,0). 若点M在点N的左边,试比较a1与a2的大小.
查看答案和解析>>
科目: 来源:2012届广东省珠海市紫荆中学九年级第二次模拟考试数学卷(带解析) 题型:解答题
如图,直线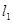 交直线
交直线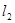 于
于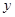 轴上一点
轴上一点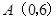 ,交
,交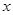 轴上另一点
轴上另一点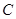 ,
,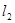 交
交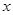 轴于另一点
轴于另一点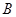 ,二次函数
,二次函数 (
(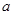 >0)的图像过点
>0)的图像过点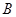 、
、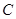 两点,点
两点,点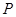 是线段
是线段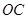 上由
上由 向
向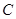 移动的动点,线段
移动的动点,线段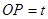 (1<
(1<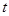 <8)。
<8)。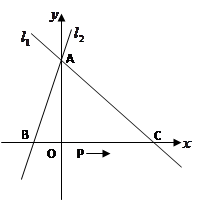
⑴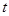 为何值时,
为何值时,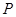 为圆心
为圆心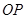 为半径的圆与
为半径的圆与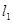 相切;
相切;
⑵设抛物线对称轴与直线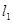 相交于点
相交于点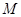 ,请在
,请在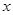 轴上求一点
轴上求一点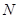 ,使
,使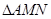 的周长最小;
的周长最小;
⑶设点 是
是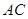 上由
上由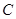 向
向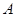 移动的一动点,且
移动的一动点,且 ,若
,若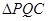 的面积为
的面积为 ,求
,求 与
与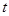 的函数关系式,当
的函数关系式,当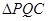 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出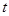 的值。
的值。
查看答案和解析>>
科目: 来源:2012届广东省广州市番禺区中考一模数学卷(带解析) 题型:解答题
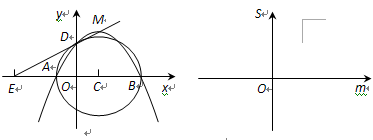
已知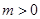 ,点
,点 的坐标为
的坐标为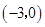 ,关于
,关于 的二次函数
的二次函数 图象的顶点为
图象的顶点为 ,图象交
,图象交 轴于
轴于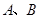 两点,交
两点,交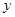 轴正半轴于
轴正半轴于 点.以
点.以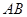 为直径作圆,其圆心为
为直径作圆,其圆心为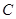 .
. 
(1)写出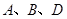 三点的坐标(可用含
三点的坐标(可用含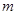 的代数式表示);
的代数式表示);
(2)当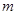 为何值时
为何值时 点在直线
点在直线 上?判定此时直线
上?判定此时直线 与圆的位置关系?
与圆的位置关系?
(3)连接 ,当
,当 变化时,试用
变化时,试用 表示
表示 的面积
的面积 ,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
查看答案和解析>>
科目: 来源:2012届江苏省南通一中九年级中考适应性考试(三)数学卷(带解析) 题型:解答题
已知:如图,在平面直角坐标系 中,矩形OABC的边OA在
中,矩形OABC的边OA在 轴的正半轴上,OC在
轴的正半轴上,OC在 轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。
轴的正半轴上,OA=2,OC=3。过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E。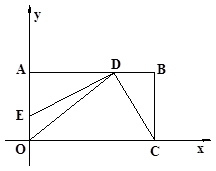
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与 轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为
轴的正半轴交于点F,另一边与线段OC交于点G。如果DF与(1)中的抛物线交于另一点M,点M的横坐标为 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源:2012届江苏涟水实验中学中考模拟数学试卷(带解析) 题型:解答题
已知二次函数y =" -" x2 - x +
【小题1】在给定的直角坐标系中,画出这个函数的图象;
【小题2】根据图象,写出当y < 0时,x的取值范围
【小题3】若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式
查看答案和解析>>
科目: 来源:2012届湖北天门九年级毕业考试数学试卷(带解析) 题型:解答题
如图,抛物线 与
与 轴交于A、B两点,与y轴交于C点,且
轴交于A、B两点,与y轴交于C点,且 .
.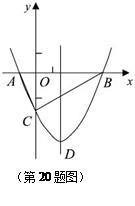
【小题1】求抛物线的解析式及顶点D的坐标;
【小题2】点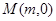 是
是 轴上的一个动点,当的
轴上的一个动点,当的 值最小
值最小
时,求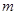 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com