
科目: 来源:2012届浙江省温州初中生学业考试数学试卷(带解析) 题型:解答题
如图,经过原点的抛物线 与
与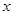 轴的另一个交点为A.过点
轴的另一个交点为A.过点 作直线
作直线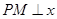 轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
【小题1】当 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
【小题2】当 时,连结CA,问
时,连结CA,问 为何值时
为何值时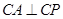 ?
?
【小题3】过点P作 且
且 ,问是否存在
,问是否存在 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的 的值,并定出相对应的点E坐标;若不存在,请说明理由。
的值,并定出相对应的点E坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源:2012届福建省福州市初中毕业班质量检查数学卷(带解析) 题型:解答题
如图,已知抛物线 经过A(3,0)、B(0,4)
经过A(3,0)、B(0,4)
(1)求此抛物线的解析式;
(2)若抛物线与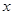 轴的另一个交点为C,求点C关于直线AB的对称点
轴的另一个交点为C,求点C关于直线AB的对称点 的坐标;
的坐标;
(3)若点C是第二象限内一点,以点D为圆心的圆分别与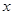 轴、
轴、 轴、直线AB相切于点E、F、H,问在抛物线的对称轴上是否存在一点P,使得
轴、直线AB相切于点E、F、H,问在抛物线的对称轴上是否存在一点P,使得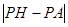 的值最大?若存在,求出该最大值;若不存在,请说明理由。
的值最大?若存在,求出该最大值;若不存在,请说明理由。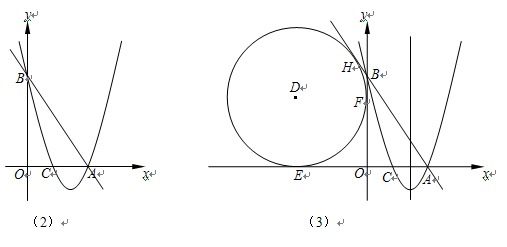
查看答案和解析>>
科目: 来源:2012届贵州省遵义市中考模拟数学卷(带解析) 题型:解答题
已知二次函数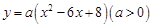 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
(1)如图①,连接AC,将△OAC沿直线AC翻折,若点O的对应点O'恰好落在该抛物线的对称轴上,求实数a的值;
(2)如图②,在正方形EFGH中,点E、F的坐标分别是(4,4)、(4,3),边HG位于边EF的右侧.若点P是边EF或边FG上的任意一点,求证四条线段PA、PB、PC、PD不能构成平行四边形;
(3)如图②,正方形EFGH向左平移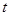 个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出
个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出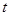 的取值范围.
的取值范围.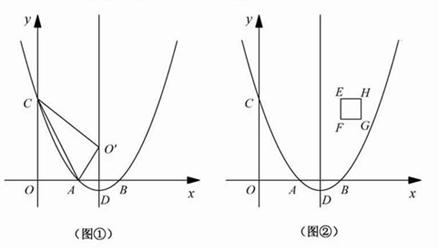
查看答案和解析>>
科目: 来源:2012年湖北省汉川市马口中学中考模拟数学试卷(带解析) 题型:解答题
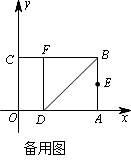
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为 顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周 长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.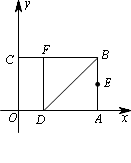
查看答案和解析>>
科目: 来源:2012届河南省虞城县营盘中学中考模拟三数学卷(带解析) 题型:解答题
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量 (件)与销售单价
(件)与销售单价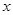 (元)符合一次函数
(元)符合一次函数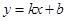 ,且
,且 时,
时, ;
; 时,
时, .
.
(1)求一次函数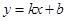 的表达式;
的表达式;
(2)若该商场获得利润为 元,试写出利润
元,试写出利润 与销售单价
与销售单价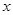 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价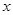 的范围.
的范围.
查看答案和解析>>
科目: 来源:2012年广西柳州市初三毕业学业考试模拟考试数学试卷(带解析) 题型:解答题
平面直角坐标系xOy中,抛物线 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为 (1, 0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为 (1, 0),OB=OC,抛物线的顶点为D.
(1) 求此抛物线的解析式;
(2) 若此抛物线的对称轴上的点P满足∠APB=∠ACB,求点P的坐标;
(3) Q为线段BD上一点,点A关于∠AQB的平分线的对称点为 ,若
,若 ,求点Q的坐标和此时△
,求点Q的坐标和此时△ 的面积.
的面积.
查看答案和解析>>
科目: 来源:2012年广西柳州市初三毕业学业考试模拟考试数学试卷(带解析) 题型:解答题
已知关于x的一元二次方程 的一个实数根为 2.
的一个实数根为 2.
(1) 用含p的代数式表示q;
(2) 求证:抛物线 与x轴有两个交点;
与x轴有两个交点;
(3) 设抛物线 的顶点为M,与 y轴的交点为E,抛物线
的顶点为M,与 y轴的交点为E,抛物线
顶点为N,与y轴的交点为F,若四边形FEMN的面积等于2,求p的值.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(江苏苏州卷)数学(带解析) 题型:解答题
如图,已知抛物线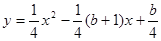 (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
【小题1】点B的坐标为 ▲ ,点C的坐标为 ▲ (用含b的代数式表示);
【小题2】请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
【小题3】请你进一步探索在第一象限内是否存在点Q,使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届天津市红桥区中考二模数学试卷(带解析) 题型:解答题
已知一抛物线经过 (0,0),
(0,0), (1,1)两点,且解析式的二次项系数为
(1,1)两点,且解析式的二次项系数为
( >0).
>0).
【小题1】当 时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
【小题2】已知点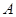 (0,1),若抛物线与射线
(0,1),若抛物线与射线 相交于点
相交于点 ,与
,与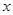 轴相交于点
轴相交于点 (异于原点),当
(异于原点),当 在什么范围内取值时,
在什么范围内取值时, 的值为常数?当
的值为常数?当 在什么范围内取值时,
在什么范围内取值时, 的值为常数?
的值为常数?
【小题3】若点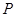 (
( ,
, )在抛物线上,则称点
)在抛物线上,则称点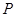 为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线 上,请说明理由.
上,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com