
科目: 来源:2012年河北省石家庄市42中学九年级第二次模拟考试数学试卷(带解析) 题型:解答题
如图1,在平面直角坐标系中,点A的坐标为(1,2),点B的坐标为(3,1),二次函数y=x2的图象记为抛物线l1.
(1)平移抛物线l1,使平移后的抛物线过点A,但不过点B,写出平移后的一个抛物线的函数表达式(任写一个即可);
(2)平移抛物线l1,使平移后的抛物线过A,B两点,记为抛物线l2,如图2,求抛物线l2的函数表达式;
(3)设抛物线l2的顶点为C,K为y轴上一点.若S△ABK=S△ABC,求点K的坐标;
(4)请在图3上用尺规作图的方式探究抛物线l2上是否存在点P,使△ABP为等腰三角形.若存在,请判断点P共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.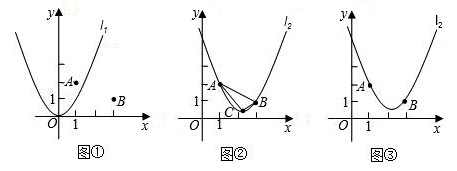
查看答案和解析>>
科目: 来源:2012年广西融安县第一次中考模拟考试数学试卷(带解析) 题型:解答题
已知,如图,抛物线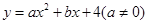 与
与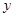 轴交于点
轴交于点 ,与
,与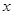 轴交于点
轴交于点 ,点
,点 的坐标为
的坐标为 ,对称轴是
,对称轴是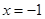 .
.
(1)求该抛物线的解析式;
(2)点 是线段
是线段 上的动点,过点
上的动点,过点 作
作 ∥
∥ ,分别交
,分别交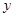 轴、
轴、 于点P、
于点P、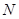 ,连接
,连接 .当
.当 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标;
(3)在(2)的条件下,求 的值.
的值.
查看答案和解析>>
科目: 来源:2012届福建厦门海沧区九年级质量检查数学试卷(带解析) 题型:解答题
已知二次函数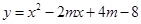 .
.
【小题1】当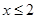 时,函数值
时,函数值 随
随 的增大而减小,求
的增大而减小,求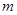 的取值范围;
的取值范围;
【小题2】以抛物线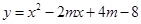 的顶点
的顶点 为一个顶点作该抛物线的内接正
为一个顶点作该抛物线的内接正 (
(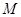 ,
,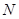 两点在抛物线上),请问:△
两点在抛物线上),请问:△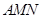 的面积是与
的面积是与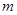 无关的定值吗?若是,请求出这个定值;若不是,请说明理由;
无关的定值吗?若是,请求出这个定值;若不是,请说明理由;
【小题3】若抛物线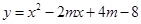 与
与 轴交点的横坐标均为整数,求整数
轴交点的横坐标均为整数,求整数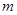 的值.
的值.
查看答案和解析>>
科目: 来源:2012届福建厦门海沧区九年级质量检查数学试卷(带解析) 题型:解答题
若一次函数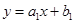 (
(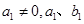 是常数)与
是常数)与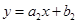 (
(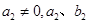 是常数),满足
是常数),满足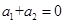 且
且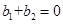 ,则称这两函数是对称函数
,则称这两函数是对称函数
【小题1】当函数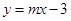 与
与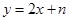 是对称函数,求
是对称函数,求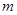 和
和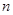 的值;
的值;
【小题2】在平面直角坐标系中,一次函数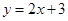 图象与
图象与 轴交于点
轴交于点 、与
、与 轴交于点
轴交于点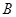 ,点
,点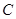 与点
与点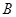 关于x轴对称,过点
关于x轴对称,过点 、
、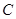 的直线解析式是
的直线解析式是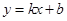 ,求证:函数
,求证:函数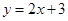 与
与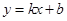 是对称函数
是对称函数
查看答案和解析>>
科目: 来源:2012届广西融安中考二模数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
【小题1】求线段OA所在直线的函数解析式
【小题2】设抛物线顶点M的横坐标为m,
①用m的代数式表示点P的坐标;
②当m为何值时,线段PB最短;
【小题3】当线段PB最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等,若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届广西融安中考二模数学试卷(带解析) 题型:解答题
已知关于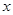 的方程
的方程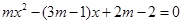 .
.
【小题1】求证:无论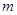 取任何实数时,方程恒有实数根;
取任何实数时,方程恒有实数根;
【小题2】若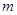 为整数,且抛物线
为整数,且抛物线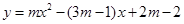 与
与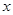 轴两交点间的距离为2,求抛物线的解析式
轴两交点间的距离为2,求抛物线的解析式
【小题3】若直线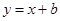 与(2)中的抛物线没有交点,求
与(2)中的抛物线没有交点,求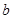 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2012届广西融安中考二模数学试卷(带解析) 题型:解答题
某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
【小题1】假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
【小题2】商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
【小题3】每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目: 来源:2012届福建厦门思明区九年级质量检查数学试卷(带解析) 题型:解答题
在平面直角坐标系中,已知函数 和函数
和函数 ,不论
,不论 取何值,
取何值, 都取
都取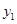 与
与 二者之中的较小值.
二者之中的较小值.
【小题1】求 关于
关于 的函数关系式
的函数关系式
【小题2】现有二次函数 ,若函数
,若函数 和
和 都随着
都随着 的增大而减小,求自变
的增大而减小,求自变
量 的取值范围
的取值范围
【小题3】在(2)的结论下,若函数 和
和 的图象有且只有一个公共点,求
的图象有且只有一个公共点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2012届福建厦门思明区九年级质量检查数学试卷(带解析) 题型:解答题
已知二次函数 的部分图象如图7所示,抛物线与
的部分图象如图7所示,抛物线与 轴的一个交点坐标为
轴的一个交点坐标为 ,对称轴为直线
,对称轴为直线 .
.
【小题1】若 ,求
,求 的值;
的值;
【小题2】若实数 ,比较
,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目: 来源:2012届云南省双柏县初中毕业水平考试模拟(二)数学卷(带解析) 题型:解答题
如图,直线y=3x+3交 轴于A点,交
轴于A点,交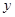 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交 轴于另一点C(3,0).(1)求抛物线的解析式;(2)求抛物线的对称轴和顶点坐标.
轴于另一点C(3,0).(1)求抛物线的解析式;(2)求抛物线的对称轴和顶点坐标. 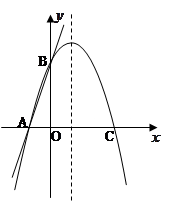
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com