
科目: 来源:2012届江苏盐城九年级中考模拟考试数学试卷(带解析) 题型:解答题
如图,抛物线经过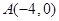 ,
,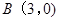 ,
,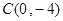 三点.
三点.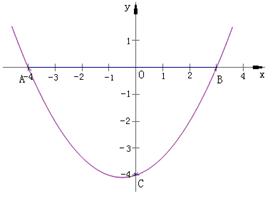
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上存在一点 ,使
,使 的值最小,求点
的值最小,求点 的坐标以
的坐标以
及 的最小值;
的最小值;
(3)在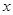 轴上取一点
轴上取一点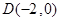 ,连接
,连接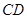 .现有一动点
.现有一动点 以每秒
以每秒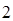 个单位长度的速度从点
个单位长度的速度从点 出发,沿线段
出发,沿线段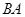 向点
向点 运动,运动时间为
运动,运动时间为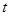 秒,另有一动点
秒,另有一动点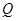 以某一速度同时从点
以某一速度同时从点 出发,沿线段
出发,沿线段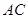 向点
向点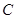 运动,当点
运动,当点 、点
、点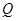 两点中有一点到达终点时,另一点则停止运动(如右图所示).在运动的过程中是否存在一个
两点中有一点到达终点时,另一点则停止运动(如右图所示).在运动的过程中是否存在一个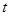 值,使线段
值,使线段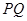 恰好被
恰好被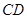 垂直平分.如果存在,请求出
垂直平分.如果存在,请求出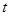 的值和点
的值和点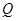 的速度,如果不存在,请说明理由.
的速度,如果不存在,请说明理由.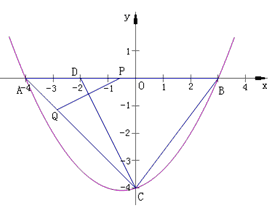
查看答案和解析>>
科目: 来源:2012届广西武鸣中考第一次模拟数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.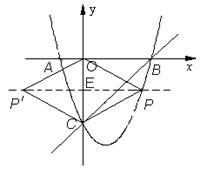
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP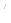 C, 那么是否存在点P,使四边形POP
C, 那么是否存在点P,使四边形POP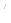 C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目: 来源:2012届湖南衡阳市初中学业水平模拟考试数学卷(带解析) 题型:解答题
如图9, 已知抛物线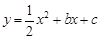 与
与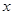 轴交于A (-4,0) 和B(1,0)两点,与
轴交于A (-4,0) 和B(1,0)两点,与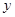 轴交于C点.
轴交于C点.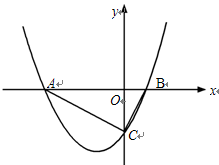
(1)求此抛物线的解析式;
(2)设E是线段AB上的动点,作EF//AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作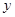 轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
查看答案和解析>>
科目: 来源:2012届浙江省四校九年级联考数学卷(带解析) 题型:解答题
在平面坐标系xoy中,直线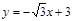 与x,y轴交于点A,B,作△AOB为外接⊙E.将直角三角板的30°角的顶点C摆放在圆弧上,三角板的两边始终过点O,A,并且不断地转动三角板.
与x,y轴交于点A,B,作△AOB为外接⊙E.将直角三角板的30°角的顶点C摆放在圆弧上,三角板的两边始终过点O,A,并且不断地转动三角板.
(1)如图1,当点C与B重合时,连接OE求扇形EOA的面积;
(2)当 时,求经过A,O,C三点的抛物线的解析式,直接写出顶点坐标;
时,求经过A,O,C三点的抛物线的解析式,直接写出顶点坐标;
(3)如图2,在转动中,过C作⊙E的切线,交y轴于D,当A,C,D,B四点围成的四边形是梯形时,求点D的坐标.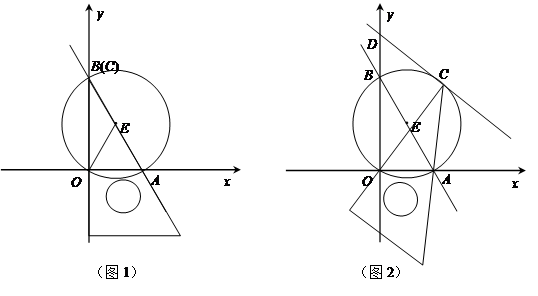
查看答案和解析>>
科目: 来源:2012届浙江省金衢十一校九年级适应性练习数学卷(带解析) 题型:解答题
已知如图,对称轴为直线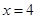 的抛物线
的抛物线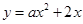 与
与 轴相交于点B、O.
轴相交于点B、O.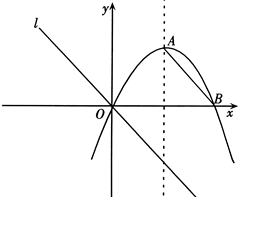
(1)求抛物线的解析式,并求出顶点A的坐标.
(2) 连结AB,平移AB所在的直线,使其经过原点O,得到直线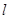 .点
.点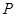 是
是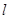 上一动点,当△
上一动点,当△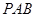 的周长最小时,求点P的坐标.
的周长最小时,求点P的坐标.
(3)当△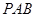 的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似,若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O)
的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似,若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O)
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(河南洛阳卷)数学(带解析) 题型:解答题
如图,在平面直角坐标系中,直线 与抛物线
与抛物线 交于A,B两点,点A在
交于A,B两点,点A在 轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作
轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作 轴的垂线交直线AB与点C,作PD⊥AB于点D
轴的垂线交直线AB与点C,作PD⊥AB于点D
(1)求 及
及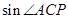 的值
的值
(2)设点P的横坐标为
①用含 的代数式表示线段PD的长,并求出线段PD长的最大值;
的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把 分成两个三角形,是否存在适合的
分成两个三角形,是否存在适合的 值,使这两个三角形的面积之比为9:10?若存在,直接写出
值,使这两个三角形的面积之比为9:10?若存在,直接写出 值;若不存在,说明理由.
值;若不存在,说明理由.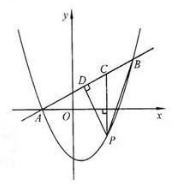
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖北武汉卷)数学(带解析) 题型:解答题
如图1,点A为抛物线C1: 的顶点,点B的坐标为(1,0),直线AB交抛物线C1于另一点C.
的顶点,点B的坐标为(1,0),直线AB交抛物线C1于另一点C.
(1)求点C的坐标;
(2)如图1,平行于y轴的直线x=3交直线AB于点D,交抛物线C1于点E,平行于y轴的直线x=a
交直线AB于F,交抛物线C1于G,若FG:DE=4∶3,求a的值;
(3)如图2,将抛物线C1向下平移m(m>0)个单位得到抛物线C2,且抛物线C2的顶点为点P,交x轴
于点M,交射线BC于点N,NQ⊥x轴于点Q,当NP平分∠MNQ时,求m的值.

图1 图2
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖北武汉卷)数学(带解析) 题型:解答题
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系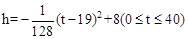 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?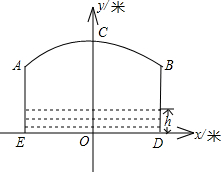
查看答案和解析>>
科目: 来源:2012届浙江省兰溪市柏社中学九年级下学期独立作业数学卷(带解析) 题型:解答题
已知抛物线y=﹣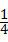 x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.
x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.
(1)请求出抛物线的解析式,并求出点A的坐标.
(2)在抛物线上是否存在点M,使得△MAB的面积等于△ABC的面积.如果存在,求出符合条件的点M的坐标;如果不存在,请说明理由.
(3)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一 个顶点E在PQ上.请求出此时点Q的坐标和直线BQ的函数解析式;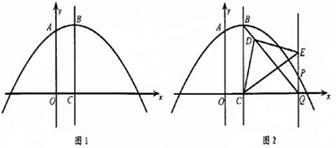
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.
查看答案和解析>>
科目: 来源:2012届浙江省兰溪市柏社中学九年级下学期独立作业数学卷(带解析) 题型:解答题
定义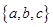 为函数
为函数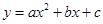 的“特征数”.如:函数
的“特征数”.如:函数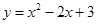 的“特征数”是
的“特征数”是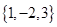 ,函数
,函数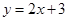 的“特征数”是
的“特征数”是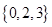 ,函数
,函数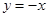 的“特征数”是
的“特征数”是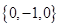

(1)将“特征数”是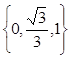 的函数图象向下平移2个单位,得到一个新函数,这个新
的函数图象向下平移2个单位,得到一个新函数,这个新
函数的解析式是 ;
(2)在(1)中,平移前后的两个函数分别与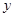 轴交于A、B两点,与直线
轴交于A、B两点,与直线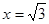 分别交于
分别交于
D、C两点,在给出的平面直角坐标系中画出图形,判断以A、B、C、D四点为顶点的四边形形状,并说明理由;
(3)若(2)中的四边形与“特征数”是的函数图象有交点,试求出实数
b 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com