
科目: 来源:2012届广东省汕头市峡山街道模拟考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,矩形OABC的顶点A(0,3)、C(-1,0).将矩形OABC绕原点O顺时针方向旋转90o,得到矩形OA′B′C′.设直线BB′与x轴交于点M、与y轴交于点N,抛物线经过点C、M、N.解答下列问题:
(1)求直线BB′的 函数解析式;
(2)求抛物线的解析式;
(3)在抛物线上求出使S△PB′′ C′= S矩形OABC的所有点P的坐标.
S矩形OABC的所有点P的坐标. 

查看答案和解析>>
科目: 来源:2012届湖南省临武县楚江中学初中毕业学业考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系 中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴
中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴 与
与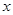 轴相交于点M.
轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)设点P为抛物线( )上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的
)上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的
正整数,请你直接写出点P的坐标;
(3)连接AC.探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求
出点N的坐标;若不存在,请你说明理由. 
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江宁波卷)数学(带解析) 题型:解答题
如图,二次函数 的图像交
的图像交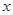 轴于
轴于 ,交
,交 轴于
轴于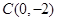 ,过
,过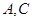 画直线。
画直线。
(1)求二次函数的解析式;
(2)点 在
在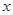 轴正半轴上,且
轴正半轴上,且 ,求
,求 的长;
的长;
(3)点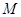 在二次函数图像上,以
在二次函数图像上,以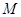 为圆心的圆与直线
为圆心的圆与直线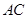 相切,切点为
相切,切点为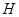 。
。
① 点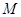 在
在 轴右侧,且
轴右侧,且 (点
(点 与点
与点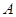 对应),求点
对应),求点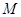 的坐标;
的坐标;
② 若 的半径为
的半径为 ,求点
,求点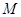 的坐标。
的坐标。
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江嘉兴卷)数学(带解析) 题型:解答题
在平面直角坐标系xOy中,点P是抛物线:y=x2上的动点(点在第一象限内).连接 OP,过点0作OP的垂线交抛物线于另一点Q.连接PQ,交y轴于点M.作PA丄x轴于点A,QB丄x轴于点B.设点P的横坐标为m.
(1)如图1,当m=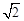 时,
时,
①求线段OP的长和tan∠POM的值;
②在y轴上找一点C,使△OCQ是以OQ为腰的等腰三角形,求点C的坐标;
(2)如图2,连接AM、BM,分别与OP、OQ相交于点D、E.
①用含m的代数式表示点Q的坐标;
②求证:四边形ODME是矩形.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江嘉兴卷)数学(带解析) 题型:解答题
某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出工辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为 元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(天津市卷)数学(带解析) 题型:解答题
已知抛物线y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,yA)、B(0,yB)、C(-1,yC)在该抛物线上.
(Ⅰ)当a=1,b=4,c=10时,①求顶点P的坐标;②求 -的值;
-的值;
(Ⅱ)当y0≥0恒成立时,求 的最小值.
的最小值.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖南长沙卷)数学(带解析) 题型:解答题
如图半径分别为m,n(0<m<n)的两圆⊙O1和⊙O2相交于P,Q两点,且点P(4,1),两圆同时与两坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.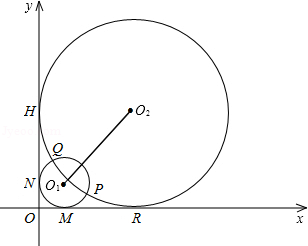
(1)求两圆的圆心O1,O2所在直线的解析式;
(2)求两圆的圆心O1,O2之间的距离d;
(3)令四边形PO1QO2的面积为S1,四边形RMO1O2的面积为S2.
试探究:是否存在一条经过P,Q两点、开口向下,且在x轴上截得的线段长为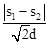 的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.
的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(广东汕头卷)数学(带解析) 题型:解答题
如图,抛物线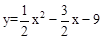 与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江金华卷)数学(带解析) 题型:解答题
如图1,已知直线y=kx与抛物线y=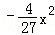
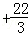 交于点A(3,6).
交于点A(3,6).
(1)求直线y=kx的解析式和线段OA的长度;
(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;
(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?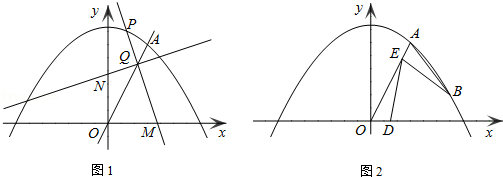
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江丽水卷)数学(带解析) 题型:解答题
在直角坐标系中,点A是抛物线y=x2在第二象限上的点,连接OA,过点O作OB⊥OA,交抛物线于点B,以OA、OB为边构造矩形AOBC.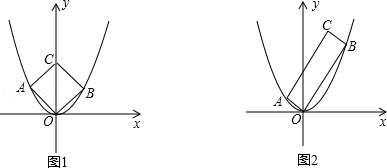
(1)如图1,当点A的横坐标为 时,矩形AOBC是正方形;
(2)如图2,当点A的横坐标为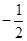 时,
时,
①求点B的坐标;
②将抛物线y=x2作关于x轴的轴对称变换得到抛物线y=-x2,试判断抛物线y=-x2经过平移交换后,能否经过A,B,C三点?如果可以,说出变换的过程;如果不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com