
科目: 来源:2012年初中毕业升学考试(浙江义乌卷)数学(带解析) 题型:解答题
如图1,已知直线y=kx与抛物线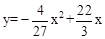 交于点A(3,6).
交于点A(3,6).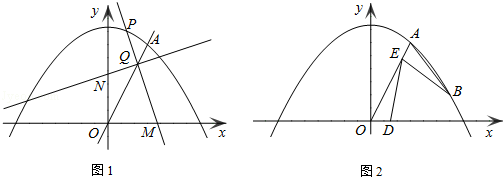
(1)求直线y=kx的解析式和线段OA的长度;
(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;
(3)如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江温州卷)数学(带解析) 题型:解答题
如图,经过原点的抛物线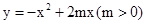 与
与 轴的另一个交点为A.过点
轴的另一个交点为A.过点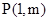 作直线
作直线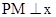 轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
(1)当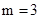 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
(2)当 时,连结CA,问
时,连结CA,问 为何值时CA⊥CP?
为何值时CA⊥CP?
(3)过点P作PE⊥PC且PE=PC,问是否存在 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的 的值,并写出相对应的点E坐标;若不存在,请说明理由。
的值,并写出相对应的点E坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江绍兴卷)数学(带解析) 题型:解答题
如图,矩形OABC的两边在坐标轴上,连接AC,抛物线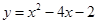 经过A,B两点。
经过A,B两点。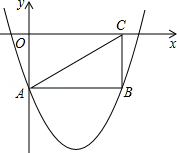
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿AO,OC,CB边向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒。
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,∠HOQ>∠POQ,求点H的纵坐标的取值范围。
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江绍兴卷)数学(带解析) 题型:解答题
把一边长为40cm的正方形硬纸板,进行适当的剪裁,折成一个长方形盒子(纸板的厚度忽略不计)。
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子。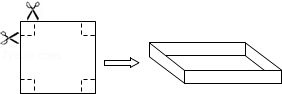
①要使折成的长方形盒子的底面积为484cm2,那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由。
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方形盒子,若折成的一个长方形盒子的表面积为550cm2,求此时长方形盒子的长、宽、高(只需求出符合要求的一种情况)。
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江衢州卷)数学(带解析) 题型:解答题
如图,把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中,使直角边OB、OD在x轴上.已知点A(1,2),过A、C两点的直线分别交x轴、y轴于点E、F.抛物线y=ax2+bx+c经过O、A、C三点.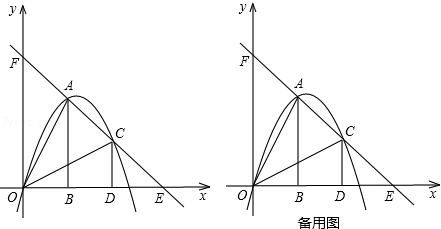
(1)求该抛物线的函数解析式;
(2)点P为线段OC上一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM为等腰梯形?若存在,求出此时点P的坐标;若不存在,请说明理由.
(3)若△AOB沿AC方向平移(点A始终在线段AC上,且不与点C重合),△AOB在平移过程中与△COD重叠部分面积记为S.试探究S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届浙江省金华市婺城区第二学期初三调研数学试卷(带解析) 题型:解答题
如图1,在直角坐标系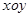 中,抛物线
中,抛物线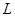 :
: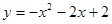 与
与 轴交于点
轴交于点 ,以
,以 为一边向左侧作正方形
为一边向左侧作正方形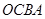 上;如图2,把正方形
上;如图2,把正方形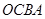 绕点
绕点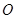 顺时针旋转
顺时针旋转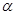 后得到正方形
后得到正方形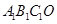 (
(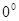 ﹤
﹤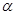 ﹤
﹤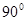 )﹒
)﹒

(1) 、
、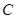 两点的坐标分别为 、 ;
两点的坐标分别为 、 ;
(2)当 tan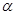 ﹦
﹦ 时,抛物线
时,抛物线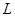 的对称轴上是否存在一点
的对称轴上是否存在一点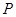 ,使△
,使△ 为直角三角形?若存在,请求出所有点
为直角三角形?若存在,请求出所有点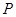 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)在抛物线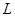 的对称轴上是否存在一点
的对称轴上是否存在一点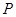 ,使△
,使△ 为等腰直角三角形?若存在,请直接写出此时tan
为等腰直角三角形?若存在,请直接写出此时tan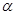 的值;若不存在,请说明理由﹒
的值;若不存在,请说明理由﹒
查看答案和解析>>
科目: 来源:2012届浙江省金华市十八中学中考模拟数学试卷(带解析) 题型:解答题
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C, D为OC的中点,直线AD交抛物线于点E(2,6),且△ABE与△ABC的面积之比为3∶2.
(1)求这条抛物线对应的函数关系式;
(2)连结BD,试判断BD与AD的位置关系,并说明理由;
(3)连结BC交直线AD于点M,在直线AD上,是否存在这样的点N(不与点M重合),使得以A、B、N为顶点的三角形与△ABM相似?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届浙江金华十八中九年级上期期中调研数学试卷(带解析) 题型:解答题
孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线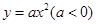 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点
的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点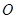 ,两直角边与该抛物线交于
,两直角边与该抛物线交于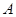 、
、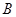 两点,请解答以下问题:
两点,请解答以下问题:
(1)若测得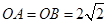 (如图1),求
(如图1),求 的值;
的值;
(2)对同一条抛物线,孔明将三角板绕点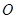 旋转到如图2所示位置时,过
旋转到如图2所示位置时,过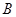 作
作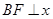 轴于点
轴于点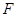 ,测得
,测得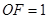 ,写出此时点
,写出此时点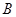 的坐标,并求点
的坐标,并求点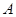 的横坐标;
的横坐标;
(3)对该抛物线,孔明将三角板绕点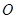 旋转任意角度时惊奇地发现,交点
旋转任意角度时惊奇地发现,交点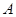 、
、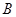 的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
的连线段总经过一个固定的点,试说明理由并求出该点的坐标.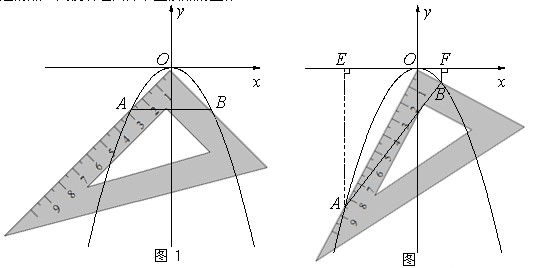
查看答案和解析>>
科目: 来源:2012届浙江金华十八中九年级上期期中调研数学试卷(带解析) 题型:解答题
某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y = x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为W内(元)(利润 = 销售额-成本-广告费).
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为W内(元)(利润 = 销售额-成本-广告费).
若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳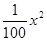 元的附加费,设月利润为W外(元)(利润 = 销售额-成本-附加费).
元的附加费,设月利润为W外(元)(利润 = 销售额-成本-附加费).
(1)当x = 1000时,y = 元/件,W内 = 元;
(2)分别求出W内,W外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值;
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?
查看答案和解析>>
科目: 来源:2012届浙江金华十八中九年级上期期中调研数学试卷(带解析) 题型:解答题
二次函数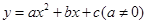 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题: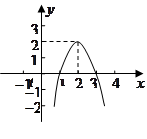
(1)写出方程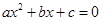 的两个根;
的两个根;
(2)当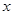 为何值时,
为何值时,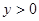 ;y﹤0;
;y﹤0;
(3)写出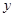 随
随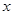 的增大而减小的自变量
的增大而减小的自变量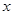 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com