
科目: 来源:2012届湖南省临武县楚江中学初中毕业学业考试模拟数学试卷1(带解析) 题型:解答题
如图已知二次函数图象的顶点为原点, 直线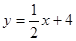 的图象与该二次函数的图象交于
的图象与该二次函数的图象交于 点(8,8),直线与
点(8,8),直线与 轴的交点为C,与y轴的交点为B.
轴的交点为C,与y轴的交点为B.
(1)求这个二次函数的解析式与B点坐标;
(2) 为线段
为线段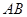 上的一个动点(点
上的一个动点(点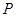 与
与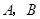 不重合),过
不重合),过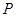 作
作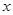 轴的垂线与这个二次函数的图象交于D点,与
轴的垂线与这个二次函数的图象交于D点,与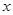 轴交于点E.设线段PD的长为
轴交于点E.设线段PD的长为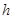 ,点
,点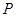 的横坐标为t,求
的横坐标为t,求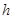 与t之间的函数关系式,并写出自变量t的取值范围;
与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,在线段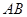 上是否存在点
上是否存在点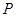 ,使得以点P、D、B为顶点的三角形与
,使得以点P、D、B为顶点的三角形与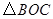 相似?若存在,请求出
相似?若存在,请求出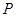 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.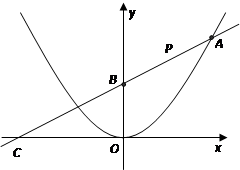
查看答案和解析>>
科目: 来源:2012届湖南省临武县楚江中学初中毕业学业考试模拟数学试卷1(带解析) 题型:解答题
某商场将进价2000元的冰箱以2400元售出,平均每天能售出8台,为配合国家“家电下乡政策的实施,商场决定采取适当的降价措施。调查表明:这种冰箱的售价每降价50元,平均每天就能多售出4台。
(1)假设每台冰箱降价x元,商场每天销售这种冰箱y台,请写出y与x的函数关系式(不要求写自变量的范围)
(2)若每台冰箱降价x元,商场每天销售这种冰箱的利润是z元,请写出z与x之间的函数表达式(不要求写自变量的取值范围);
(3)商场要想在这种冰箱销售中每天赢利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(4)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目: 来源:2012届浙江省杭州市中考数学模拟数学试卷(带解析) 题型:解答题
如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.
(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标. 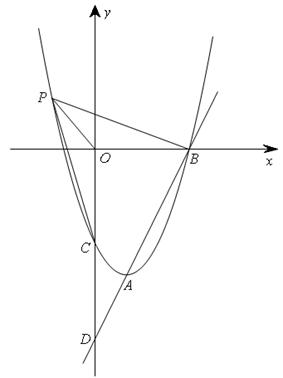
查看答案和解析>>
科目: 来源:2012届湖南临武县楚江中学初中毕业学业考试模拟(七)数学试卷(带解析) 题型:解答题
如图所示,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.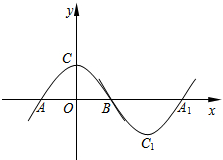
(1)当a=-1,b=1时,求抛物线n的解析式;
(2)四边形AC1A1C是什么特殊四边形,请写出结果并说明理由;
(3)若四边形AC1A1C为矩形,请求出a,b应满足的关系式.
查看答案和解析>>
科目: 来源:2012届湖南临武县楚江中学初中毕业学业考试模拟(三)数学试卷(带解析) 题型:解答题
如图,对称轴为直线x=一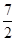 的抛物线经过点A(-6,0)和点B(0,4).
的抛物线经过点A(-6,0)和点B(0,4).
(1)求抛物线的解析式和顶点坐标;
(2)设点E(x,y)是抛物线上的一个动点,且位于第三象限,四边形OEAF是以OA为对角线的平行四边形,求□OEAF的面积S与x的函数关系式,并写出自变量x的取值范围;
①当□OEAF的面积为24时,请判断□OEAF是否为菱形?
②是否存在点E,使□OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届江苏省灌云县穆圩中学中考模拟数学试卷(带解析) 题型:解答题
如图,在坐标系中,菱形ABCD的边BC与x轴重合,点B与原点重合,AB=10, ∠ABC=60°.动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动;动点Q从点D出发沿折线DC-CB-BA以每秒3个单位长的速度匀速运动,过点P作PF⊥BC,交折线AB-AC于点E,交直线AD于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之停止,设运动时间为t秒.
(1)写出点A与点D的坐标
(2)当t=3秒时,试判断QE与AB之间的位置关系?
(3)当Q在线段DC上运动时,若△PQF为等腰三角形,求t的值;
(4)设△PQE的面积为S,求S与t的函数关系式;
查看答案和解析>>
科目: 来源:2012届江苏省灌云县穆圩中学中考模拟数学试卷(带解析) 题型:解答题
今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
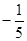 x+2.试问4月份与5月份分别在哪一周销
x+2.试问4月份与5月份分别在哪一周销查看答案和解析>>
科目: 来源:2012届河南信阳市二中中考模拟考试数学试卷(带解析) 题型:解答题
已知:抛物线 (a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0,
(a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0,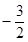 ),与x轴交于A、B两点(A在B的左边).
),与x轴交于A、B两点(A在B的左边).
(1)求此抛物线的表达式;
(2)点P是线段OB上一动点(不与点B重合),点Q在线段BM上移动且∠MPQ=45°,设线段OP=x,MQ=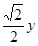 1,求y1与x的函数关系式,并写出自变量x的取值范围;
1,求y1与x的函数关系式,并写出自变量x的取值范围;
(3)①在(2)的条件下是否存在点P,使△PQB是PB为底的等腰三角形,若存在试求点Q的坐标,若不存在说明理由;
②在(1)中抛物线的对称轴上是否存在点F,使△BMF是等腰三角形,若存在直接写出所有满足条件的点F的坐标.
查看答案和解析>>
科目: 来源:2012届湖南省临武县楚江中学初中毕业学业考试模拟数学试卷6(带解析) 题型:解答题
如图,已知抛物线经过定点A(1,0),它的顶点P是y轴正半轴上的一个动点,
P点关于x轴的对称点为P′,过P′ 作x轴的平行线交抛物线于B、D两点(B点在y轴右
侧),直线BA交y轴于C点.按从特殊到一般的规律探究线段CA与CB的比值:
(1)当P点坐标为(0,1)时,写出抛物线的解析式并求线段CA与CB的比值;
(2)若P点坐标为(0,m)时(m为任意正实数),线段CA与CB的比值是否与⑴所求的比值相同?请说明理由.
查看答案和解析>>
科目: 来源:2012届湖南省临武县楚江中学初中毕业学业考试模拟数学试卷9(带解析) 题型:解答题
在平面直角坐标系中,抛物线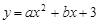 与
与 轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)直接填写: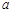 = ,b= ,顶点C的坐标为 ;
= ,b= ,顶点C的坐标为 ;
(2)在 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标. 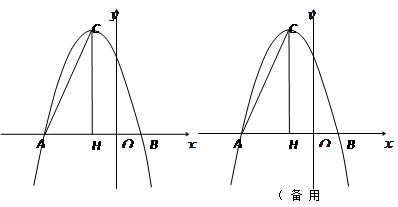
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com