
科目: 来源:2012届江苏省南通市第一初级中学九年级第一次模拟考试数学试卷(带解析) 题型:解答题
已知:直角坐标系xoy中,将直线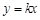 沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线
沿y轴向下平移3个单位长度后恰好经过B(-3,0)及y轴上的C点.若抛物线 与
与 轴交于A,B两点(点A在点B的右侧),且经过点C,
轴交于A,B两点(点A在点B的右侧),且经过点C,
(1)求直线 的解析式;
的解析式;
(2)求抛物线的解析式;
(3)设抛物线的顶点为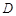 ,点
,点 在抛物线的对称轴上,且
在抛物线的对称轴上,且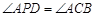 ,求点
,求点 的坐标;
的坐标;
查看答案和解析>>
科目: 来源:2012届浙江省丽水市中考模拟试卷5数学试卷(带解析) 题型:解答题
已知二次函数y=-x2+4x+5图像交x轴于点A、B,交y轴于点C,点D是该函数图像上一点,且点D的横坐标为4,连BD,点P是AB上一动点(不与点A重合),过P作PQ⊥AB交射线AD于点Q,以PQ为一边在PQ的右侧作正方形PQMN.设点P的坐标为(t,0).
(1)求点B,C,D的坐标及射线AD的解析式;
(2)在AB上是否存在点P,使⊿OCM为等腰三角形?若存在,求正方形PQMN的边长;若不存在,请说明理由;
(3)设正方形PQMN与⊿ABD重叠部分面积为s,求s与t的函数关系式.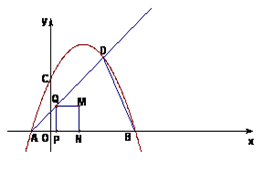
查看答案和解析>>
科目: 来源:2012届浙江省丽水市中考模拟试卷2数学试卷(带解析) 题型:解答题
已知二次函数y=x2+bx+c与x轴交于A(-1,0)、B(1,0)两点.
(1)求这个二次函数的关系式;
(2)若有一半径为r的⊙P,且圆心P在抛物线上运动,当⊙P与两坐标轴都相切时,求半径r的值.
(3)半径为1的⊙P在抛物线上,当点P的纵坐标在什么范围内取值时,⊙P与y轴相离、相交? 
查看答案和解析>>
科目: 来源:2012届浙江省丽水市中考模拟试卷2数学试卷(带解析) 题型:解答题
我市某品牌服装公司生产的玩具4月份每件生产成本为50元,5、6月每件玩具生产成本平均降低的百分率为x.
(1)用含x的代数式表示5月份每件玩具的生产成本;
(2)如果6月份每件生产成本比4月份少9.5元,试求x的值;
(3)该玩具5月份每件的销售价为60元,6月份每件的销售价比5月份有所下降,若下降的百分率与5、6月份每件玩具平均降低成本的百分率相同,且6月份每件玩具的销售价不低于48元,设6月份每件玩具获得的利润为y元,试求y与x的函数关系式,并确定单件利润y的最大值.(注:利润=销售价-生产成本)
查看答案和解析>>
科目: 来源:2012届江苏省淮安市清浦区清浦中学中考模拟试卷3数学试卷(带解析) 题型:解答题
随着我市近几年城市园林绿化建设的快速发展,对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资成本x成正比例关系,如图①所示;种植花卉的利润y2与投资成本x成二次函数关系,如图②所示(注:利润与投资成本的单位:万元)
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户计划以8万元资金投入种植花卉和树木,请求出他所获得的总利润Z与投入种植花卉的投资量x之间的函数关系式,并回答他至少获得多少利润?他能获取的最大利润是多少?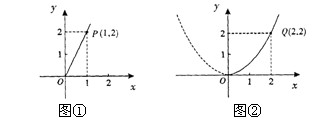
查看答案和解析>>
科目: 来源:2012届江苏省淮安市清浦区清浦中学中考模拟试卷2数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,矩形OABC的顶点A(0,3),C( ,0).将矩形OABC绕原点顺时针旋转90°,得到矩形
,0).将矩形OABC绕原点顺时针旋转90°,得到矩形 .设直线
.设直线 与
与 轴交于点M、与
轴交于点M、与 轴交于点N,抛物线
轴交于点N,抛物线 的图象经过点C、M、N.解答下列问题:
的图象经过点C、M、N.解答下列问题:
(1)分别求出直线 和抛物线所表示的函数解析式;
和抛物线所表示的函数解析式;
(2)将△MON沿直线MN翻折,点O落在点P处,请你判断点P是否在抛物线上,说明理由.
(3)将抛物线进行平移,使它经过点 ,求此时抛物线的解析式.
,求此时抛物线的解析式.
查看答案和解析>>
科目: 来源:2012届江苏省淮安市清浦区清浦中学中考模拟数学试卷(带解析) 题型:解答题
如图①, 已知抛物线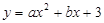 (a≠0)与
(a≠0)与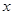 轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
(1) 求抛物线的解析式;
(2) 点D的坐标为(-2,0).问:直线AC上是否存在点F,使得△ODF是等腰三角形?若存在,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
(3) 如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求△BCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目: 来源:2012届江苏省淮安市清浦区清浦中学中考模拟数学试卷(带解析) 题型:解答题
如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线//BC,交直线CD于点F.将直线向右平移,设平移距离BE为 (t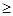 0),直角梯形ABCD被直线扫过的面积(图中阴影部份)为S,S关于的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
0),直角梯形ABCD被直线扫过的面积(图中阴影部份)为S,S关于的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.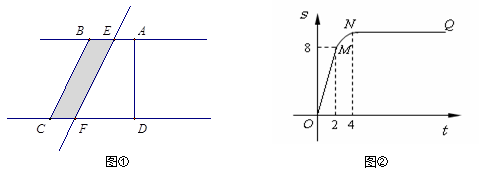
信息读取
(1)梯形上底的长AB= ;
(2) 直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4) 当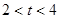 时,求S关于的函数关系式;
时,求S关于的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
查看答案和解析>>
科目: 来源:2012届河北省保定市易县九年级第二次模拟检测数学试卷(带解析) 题型:解答题
某政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+n.
(1)当销售单价x定为25元时,李明每月获得利润为w为1250元,则n= ;
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)当销售单价定为多少元时,每月可获得最大利润?并求最大利润为多少元.
查看答案和解析>>
科目: 来源:2012届河北省保定市易县九年级第一次模拟检测数学试卷(带解析) 题型:解答题
如图,抛物线y=(x+1)2+k 与x轴交于A、B两点,与y轴交于点C (0,-3).
(1)求抛物线的对称轴及k的值;
(2)抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上一动点,且在第三象限.当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标;
(4)若点E在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F为顶点的的四边形为平行四边形?若存在,直接写出出所有满足条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com