
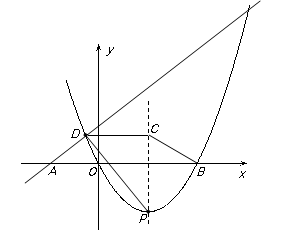
科目: 来源:2012年初中毕业升学考试(湖北宜昌卷)数学(带解析) 题型:解答题
如图,在平面直角坐标系中,直线y=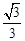 x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x﹣m)2+n经过点E.⊙M与x轴、直线AB都相切,其半径为3(1﹣
x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x﹣m)2+n经过点E.⊙M与x轴、直线AB都相切,其半径为3(1﹣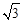 )a.
)a.
(1)求点A的坐标和∠ABO的度数;
(2)当点C与点A重合时,求a的值;
(3)点C移动多少秒时,等边△CDE的边CE第一次与⊙M相切?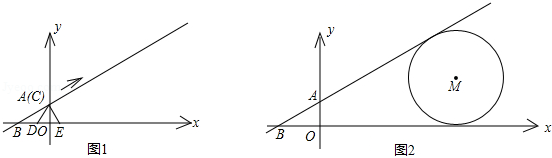
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖南岳阳卷)数学(带解析) 题型:解答题
我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直接坐标系如图①所示,如果把锅纵断面的抛物线的记为C1,把锅盖纵断面的抛物线记为C2.
(1)求C1和C2的解析式;
(2)如图②,过点B作直线BE:y=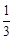 x﹣1交C1于点E(﹣2,﹣
x﹣1交C1于点E(﹣2,﹣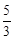 ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
(3)如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.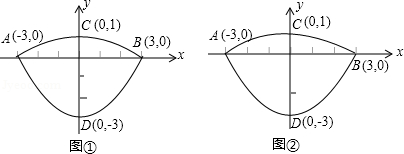
查看答案和解析>>
科目: 来源:2012届河北省邢台市初中毕业生升学第二次模拟考试数学试卷(带解析) 题型:解答题
如图,四边形ABCD是梯形,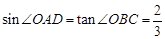 ,PC是抛物线的对称轴,且
,PC是抛物线的对称轴,且 .
.
(1)求抛物线的函数表达式;
(2)求点D的坐标;
(3)求直线AD的函数表达式;
(4)PD与AD垂直吗?
查看答案和解析>>
科目: 来源:2012届江苏省江阴市南菁中学九年级5月中考适应性训练(二模)数学试卷(带解析) 题型:解答题
已知:如图,二次函数y=a(x+1)2-4的图象与x轴分别交于A、B两点,与y轴交于点D,点C是二次函数y=a(x+1)2-4的图象的顶点,CD=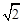 .
.
(1)求a的值.
(2)点M在二次函数y=a(x+1)2-4图象的对称轴上,且∠AMC=∠BDO,求点M的坐标.
(3)将二次函数y=a(x+1)2-4的图象向下平移k(k>0)个单位,平移后的图象与直线CD分别交于E、F两点(点F在点E左侧),设平移后的二次函数的图象的顶点为C1,与y轴的交点为D1,是否存在实数k,使得CF⊥FC1,若存在,求出k的值;若不存在,请说明理由.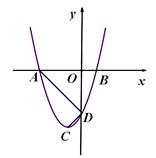
查看答案和解析>>
科目: 来源:2012届山东省聊城市高唐县九年级上学期期末考试数学试卷(带解析) 题型:解答题
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(陕西卷)数学(带解析) 题型:解答题
如果一条抛物线 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线 的“抛物线三角形”是等腰直角三角形,求
的“抛物线三角形”是等腰直角三角形,求 的值;
的值;
(3)如图,△ 是抛物线
是抛物线 的“抛物线三角形”,是否存在以原点
的“抛物线三角形”,是否存在以原点 为对称中心的矩形
为对称中心的矩形 ?若存在,求出过
?若存在,求出过 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(江西卷)数学(带解析) 题型:解答题
如图,已知二次函数L1:y=x2﹣4x+3与x轴交于A.B两点(点A在点B左边),与y轴交于点C.
(1)写出二次函数L1的开口方向、对称轴和顶点坐标;
(2)研究二次函数L2:y=kx2﹣4kx+3k(k≠0).
①写出二次函数L2与二次函数L1有关图象的两条相同的性质;
②若直线y=8k与抛物线L2交于E、F两点,问线段EF的长度是否发生变化?如果不会,请求出EF的长度;如果会,请说明理由.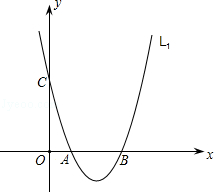
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(贵州卷)数学(带解析) 题型:解答题
如图,已知:直线 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
(1)求抛物线的解析式;
(2)若点D的坐标为(-1,0),在直线 上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使ΔADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届福建省泉州市九年级升学考试(样卷)数学试卷(带解析) 题型:解答题
如图1,在第一象限内,直线 与过点
与过点 且平行于
且平行于 轴的直线
轴的直线 相交于点
相交于点 ,半径为
,半径为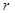 的⊙
的⊙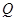 与直线
与直线 、
、 轴分别相切于点
轴分别相切于点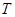 、
、 ,且与直线
,且与直线 分别交于不同的
分别交于不同的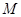 、
、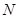 两点.
两点.
(1)当点A的坐标为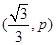 时,
时,
① 填空: = ,
= ,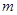 = ,
= ,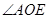 = ;
= ;
②如图2,连结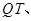
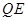 ,
,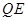 交直线
交直线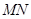 于
于 ,当
,当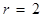 时,试说明以
时,试说明以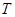 、
、 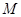 、
、 、
、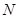 为顶点的四边形是等腰梯形;
为顶点的四边形是等腰梯形;
(2)在图1中,连结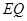 并延长交⊙
并延长交⊙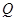 于点
于点 ,试探索:对不同的
,试探索:对不同的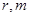 取值,经过
取值,经过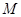 、
、 、
、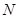 三点的抛物线
三点的抛物线 ,
, 的值会变化吗?若不变,求出
的值会变化吗?若不变,求出 的值;若变化,请说明理由.
的值;若变化,请说明理由.
查看答案和解析>>
科目: 来源:2012届浙江省丽水市青田县中考模拟数学试卷(带解析) 题型:解答题
我市某服装厂主要做外贸服装,由于技术改良,2011年全年每月的产量y(单位:万件)与月份x之间可以用一次函数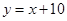 表示,但由于“欧债危机”的影响,销售受困,为了不使货积压,老板只能是降低利润销售,原来每件可赚10元,从1月开始每月每件降低0.5元。试求:
表示,但由于“欧债危机”的影响,销售受困,为了不使货积压,老板只能是降低利润销售,原来每件可赚10元,从1月开始每月每件降低0.5元。试求:
(1)几月份的单月利润是108万元?
(2)单月最大利润是多少?是哪个月份?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com