
科目: 来源:2012年初中毕业升学考试(湖南张家界卷)数学(带解析) 题型:解答题
如图,抛物线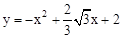 与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
(1)分别求出点A.点B的坐标;
(2)求直线AB的解析式;
(3)若反比例函数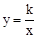 的图象过点D,求k值;
的图象过点D,求k值;
(4)两动点P、Q同时从点A出发,分别沿AB.AO方向向B.O移动,点P每秒移动1个单位,点Q每秒移动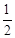 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(四川广安卷)数学(带解析) 题型:解答题
如图,在平面直角坐标系xOy中,AB⊥x轴于点B,AB=3,tan∠AOB=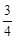 ,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
(1)求抛物线的解析式.
(2)在第三象限内,抛物线上的点P在什么位置时,△PBB1的面积最大?求出这时点P的坐标.
(3)在第三象限内,抛物线上是否存在点Q,使点Q到线段BB1的距离为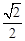 ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.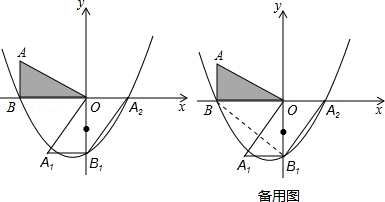
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(海南省I卷)数学(带解析) 题型:解答题
如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,
OA交其对称轴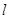 于点M,点M、N关于点P对称,连接AN、ON
于点M,点M、N关于点P对称,连接AN、ON
(1)求该二次函数的关系式.
(2)若点A的坐标是(6,-3),求△ANO的面积.
(3)当点A在对称轴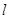 右侧的二次函数图象上运动,请解答下列问题:
右侧的二次函数图象上运动,请解答下列问题:
①证明:∠ANM=∠ONM
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标,如果不能,请说明理由.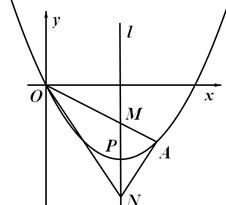
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(贵州安顺卷)数学(带解析) 题型:解答题
如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.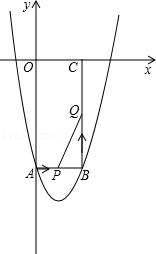
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(江苏常州卷)数学(带解析) 题型:解答题
某商场购进一批L型服装(数量足够多),进价为40元/件,以60元/件销售,每天销售20件。根据市场调研,若每件每降1元,则每天销售数量比原来多3件。现商场决定对L型服装开展降价促销活动,每件降价x元(x为正整数)。在促销期间,商场要想每天获得最大销售利润,每件降价多少元?每天最大销售毛利润为多少?(注:每件服装销售毛利润指每件服装的销售价与进货价的差)
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(福建莆田卷)数学(带解析) 题型:解答题
如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线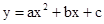
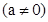 过点A。
过点A。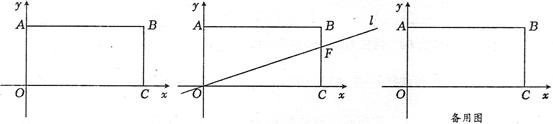
(1)(2分)求c的值; .
(2)(6分)若a=-l,且抛物线与矩形有且只有三个交点A、D、E,求△ADE的面积S的最大值;
(3)(6分)若抛物线与矩形有且只有三个交点A、M、N,线段MN的垂直平分线l过点O,交线段BC于点
F。当BF=1时,求抛物线的解析式.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖南益阳卷)数学(带解析) 题型:解答题
已知:如图,抛物线y=a(x﹣1)2+c与x轴交于点A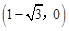 和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P'作x轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比 (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: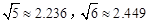 ,结果可保留根号)
,结果可保留根号)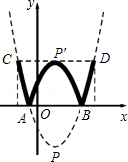
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖北天门、仙桃、潜江、江汉油田卷)数学(带解析) 题型:解答题
如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.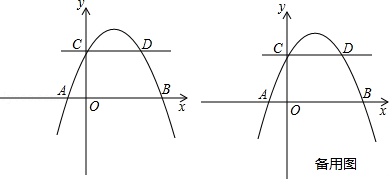
(1)求抛物线解析式及点D坐标;
(2)点E在x轴上,若以A,E,D,P为顶点的四边形是平行四边形,求此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.是否存在点P,使Q′恰好落在x轴上?若存在,求出此时点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖南娄底卷)数学(带解析) 题型:解答题
如图,在△ABC中,AB=AC,∠B=30°,BC=8,D在边BC上,E在线段DC上,DE=4,△DEF是等边三角形,边DF交边AB于点M,边EF交边AC于点N.
(1)求证:△BMD∽△CNE;
(2)当BD为何值时,以M为圆心,以MF为半径的圆与BC相切?
(3)设BD=x,五边形ANEDM的面积为y,求y与x之间的函数解析式(要求写出自变量x的取值范围);当x为何值时,y有最大值?并求y的最大值.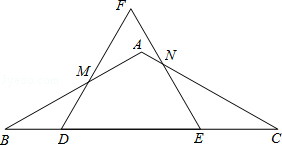
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖南娄底卷)数学(带解析) 题型:解答题
已知二次函数y=x2﹣(m2﹣2)x﹣2m的图象与x轴交于点A(x1,0)和点B(x2,0),x1<x2,与y轴交于点C,且满足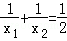 .
.
(1)求这个二次函数的解析式;
(2)探究:在直线y=x+3上是否存在一点P,使四边形PACB为平行四边形?如果有,求出点P的坐标;如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com