
科目: 来源:2012年初中毕业升学考试(贵州黔西南卷)数学(带解析) 题型:解答题
如图,在平面直角坐标系xOy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线的对称轴l与x轴相交于点M.
(1)求抛物线对应的函数解析式和对称轴;
(2)设点P为抛物线(x>5)上的一点,若以A、O、M、P为顶点的四边形的四条边的长度为四个连续的正整数,请你直接写出点P的坐标;
(3)连接AC,探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请说明理由.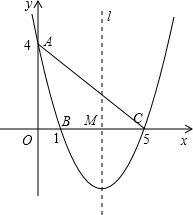
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(贵州贵阳卷)数学(带解析) 题型:解答题
如图,二次函数y=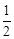 x2﹣x+c的图象与x轴分别交于A、B两点,顶点M关于x轴的对称点是M′.
x2﹣x+c的图象与x轴分别交于A、B两点,顶点M关于x轴的对称点是M′.
(1)若A(﹣4,0),求二次函数的关系式;
(2)在(1)的条件下,求四边形AMBM′的面积;
(3)是否存在抛物线y=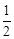 x2﹣x+c,使得四边形AMBM′为正方形?若存在,请求出此抛物线的函数关系式;若不存在,请说明理由.
x2﹣x+c,使得四边形AMBM′为正方形?若存在,请求出此抛物线的函数关系式;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届江西省南昌市十四校九年级第一次联考数学试卷(带解析) 题型:解答题
已知抛物线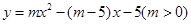 与x轴交于两点
与x轴交于两点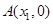 、
、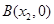
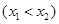 ,与y轴交于点C,AB=6.
,与y轴交于点C,AB=6.
(1)求抛物线和直线BC的解析式.
(2)在给定的直角坐标系中,画出抛物线和直线BC.
(3)若⊙P过A、B、C三点,求⊙P的半径.
(4)抛物线上是否存在点M,过点M作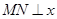 轴于点N,使
轴于点N,使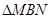 被直线BC分成面积比为
被直线BC分成面积比为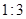 的两部
的两部
分?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届浙江省丽水市庆元县中考模拟数学试卷(带解析) 题型:解答题
已知二次函数y=x2+2x+m的图象C1与x轴有且只有一个公共点.
(1)求C1的顶点坐标;
(2)将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(﹣3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;
查看答案和解析>>
科目: 来源:2012届湖北省广水市城郊中心中学九年级下学期月考数学试卷(带解析) 题型:解答题
在平面直角坐标系中,现将一块等腰直角三角形ABC放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),如图所示;抛物线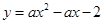 经过点B。
经过点B。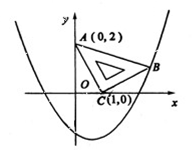
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使ΔACP仍然是以AC为直角边的等腰直角三角形?若存在,求所以点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江湖州卷)数学(带解析) 题型:解答题
如图1,已知菱形ABCD的边长为 ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(-
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(-  ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF、AF.设菱形ABCD平移的时间为t秒(0<t< 3 )
①是否存在这样的t,使△ADF与△DEF相似?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(写出答案即可)
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(浙江台州卷)数学(带解析) 题型:解答题
某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
| 时间t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
| 行驶距离s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
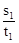 与
与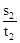 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(四川资阳卷)数学(带解析) 题型:解答题
抛物线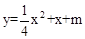 的顶点在直线
的顶点在直线 上,过点F(-2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
上,过点F(-2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
(1)(3分)先通过配方求抛物线的顶点坐标(坐标可用含m的代数式表示),再求m的值;
(2)(3分)设点N的横坐标为a,试用含a的代数式表示点N的纵坐标,并说明NF=NB;
(3)(3分)若射线NM交x轴于点P,且PA×PB=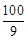 ,求点M的坐标.
,求点M的坐标.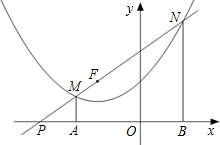
查看答案和解析>>
科目: 来源:2012届山东省临淄外国语实验学校九年级中考模拟考试(2)数学试卷(带解析) 题型:解答题
二次函数y=﹣x2+2x+m的图象与x轴交于A.B两点(B在A右侧),顶点为C,且A.B两点间的距离等于点C到x轴的距离的2倍.
(1)求此抛物线的解析式.
(2)求直线BC的解析式.
(3)若点P在抛物线的对称轴上,且⊙P与x轴以及直线BC都相切,求点P的坐标.
【提示:( +1)(
+1)( -1)=1】
-1)=1】
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖北十堰卷)数学(带解析) 题型:解答题
抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.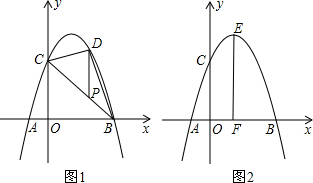
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com