
科目: 来源:2012届浙江省富阳市永兴中学九年级上学期第二次知识检测数学试卷(带解析) 题型:解答题
已知二次函数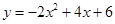 .
.
(1).求出该函数图象的顶点坐标,对称轴,并在右侧的网格中画出这个函数的大致图象。
(2)利用函数图象回答:当x在什么范围内时,y>0?
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(山东青岛卷)数学(带解析) 题型:解答题
在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元
/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润.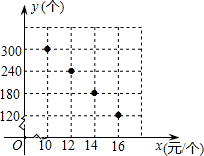
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(山东东营卷)数学(带解析) 题型:解答题
已知抛物线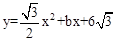 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线 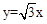 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.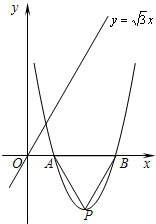
查看答案和解析>>
科目: 来源:2012届上海市奉贤区九年级调研测试数学试卷(带解析) 题型:解答题
已知:直角坐标平面内有点 ,过原点
,过原点 的直线
的直线 ,且与过点
,且与过点 、
、 的抛物线相交于第一象限的
的抛物线相交于第一象限的 点,若
点,若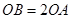 .
.
(1)求抛物线的解析式;
(2)作 轴于点
轴于点 ,设有直线
,设有直线 交直线
交直线 于
于 ,交抛物线于点
,交抛物线于点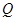 ,若
,若 、
、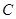 、
、 、
、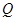 组成的四边形是平行四边形,求
组成的四边形是平行四边形,求 的值。
的值。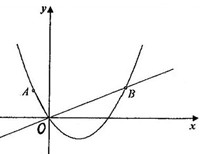
查看答案和解析>>
科目: 来源:2012届浙江省江山市中考一模数学试卷(带解析) 题型:解答题
如图1,在等腰梯形ABCD中,AB∥CO,E是AO的中点,过点E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.现把梯形ABCO放置在平面直角坐标系中,使点O与原点重合,OC在x轴正半轴上,点A、B在第一象限内。
(1) 求点E的坐标;
(2) 点P为线段EF上的一个动点,过点P作PM⊥EF交OC于点M,过M作MN∥AO交折线ABC于点N,
连结PN。设PE=x.△PMN的面积为S。
① 求S关于x的函数关系式;
② △PMN的面积是否存在最大值,若不存在,请说明理由。若存在,求出面积的最大值;
(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC)。现在开始操作:固定等腰梯形ABCO,将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动,直到点D与点C重合时停止(如图2)。设运动时间为t秒,运动后的直角梯形为E′D′G′H′;探究:在运动过程中,等腰梯形ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式。


查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(山东济南卷)数学(带解析) 题型:解答题
如图1,抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
(1)求抛物线的解析式;
(2)求cos∠CAB的值和⊙O1的半径;
(3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.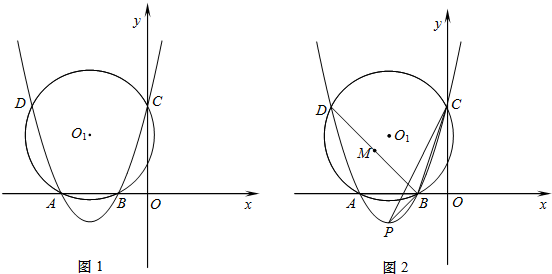
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(山东枣庄卷)数学(带解析) 题型:解答题
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠
在两坐标轴上,点C为 (-1,0).如图所示,B点在抛物线y=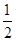 x2+
x2+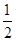 x-2图象上,过点B作
x-2图象上,过点B作
BD⊥x轴,垂足为D,且B点横坐标为-3.
(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所
有点P的坐标;若不存在,请说明理由.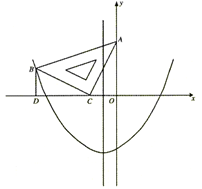
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(四川巴中卷)数学(带解析) 题型:解答题
某商品的进价为每件50元,售价为每件60元,每个月可卖出200件。如果每
件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元)。设每件商品的售价上涨x元(x
为整数),每个月的销售利润为y元,
(1)求y与x的函数关系式,并直接写出x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(贵州遵义卷)数学(带解析) 题型:解答题
如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点B的坐标为(3,﹣ ).
).
(1)求抛物线的函数解析式及点A的坐标;
(2)在抛物线上求点P,使S△POA=2S△AOB;
(3)在抛物线上是否存在点Q,使△AQO与△AOB相似?如果存在,请求出Q点的坐标;如果不存在,请说明理由.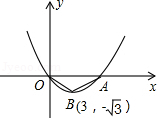
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(贵州铜仁卷)数学(带解析) 题型:解答题
如图,已知:直线 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.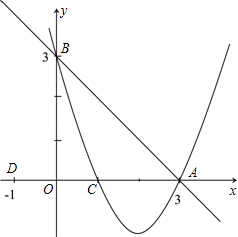
(1)求抛物线的解析式;
(2)若点D的坐标为(-1,0),在直线 上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使ΔADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com