
科目: 来源:2012届浙江省嘉兴市九年级上学期五校联考期中数学试卷(带解析) 题型:解答题
如图二次函数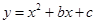 的图象经过
的图象经过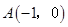 和
和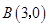 两点,且交
两点,且交 轴于点
轴于点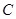 。
。
(1)试确定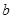 、
、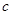 的值;
的值;
(2)过点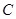 作
作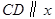 轴交抛物线于点
轴交抛物线于点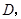 点
点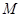 为此抛物线的顶点,试确定
为此抛物线的顶点,试确定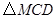 的形状。
的形状。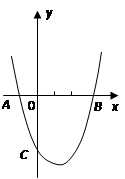
查看答案和解析>>
科目: 来源:2012届江西省吉安县文山学校九年级五科联赛选拔赛数学试卷(带解析) 题型:解答题
如图,正方形ABCD的四个顶点分别在四条平行线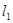 、
、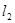 、
、 、
、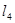 上,这四条直线中相邻两条之间的距离依次为
上,这四条直线中相邻两条之间的距离依次为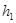 、
、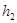 、
、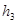 (
(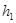 >0,
>0,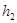 >0,
>0,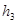 >0).
>0).
(1)求证: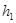 =
=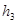 ;
;
(2)设正方形ABCD的面积为S,求证:S=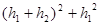 ;
;
(3)若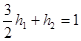 ,当
,当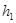 变化时,说明正方形ABCD的面积S随
变化时,说明正方形ABCD的面积S随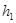 的变化情况.
的变化情况.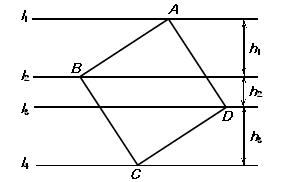
查看答案和解析>>
科目: 来源:2012届北京市门头沟区九年级上学期期末考试数学试卷(带解析) 题型:解答题
在平面直角坐标系中,抛物线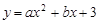 与
与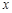 轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点坐标;
(2)在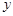 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标. 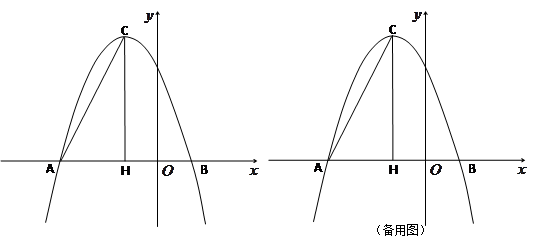
查看答案和解析>>
科目: 来源:2012届北京市门头沟区九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知抛物线 的图象向上平移m个单位(
的图象向上平移m个单位( )得到的新抛物线过点(1,8).
)得到的新抛物线过点(1,8).
(1)求m的值,并将平移后的抛物线解析式写成 的形式;
的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象. 请写出这个图象对应的函数y的解析式,同时写出该函数在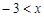 ≤
≤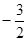 时对应的函数值y的取值范围;
时对应的函数值y的取值范围;
(3)设一次函数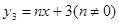 ,问是否存在正整数
,问是否存在正整数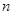 使得(2)中函数的函数值
使得(2)中函数的函数值 时,对应的x的值为
时,对应的x的值为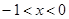 ,若存在,求出
,若存在,求出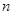 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2012届北京市门头沟区九年级上学期期末考试数学试卷(带解析) 题型:解答题
抛物线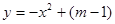 与y轴交于(0,4)点.
与y轴交于(0,4)点.
(1) 求出m的值;并画出此抛物线的图象;
(2) 求此抛物线与x轴的交点坐标;
(3) 结合图象回答:x取什么值时,函数值y>0?
查看答案和解析>>
科目: 来源:2011届浙江省温州瓯北学区九年级四科综合测试数学试卷(带解析) 题型:解答题
如图,已知抛物线y = ax2 + bx-4与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为 .
.
(1)求m的值及抛物线的解析式;
(2)点P是线段 上的一个动点,过点P作PN∥
上的一个动点,过点P作PN∥ ,交
,交 于点
于点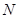 ,连接CP,当
,连接CP,当 的面积最大时,求点P的坐标;
的面积最大时,求点P的坐标;
(3)点 在(1)中抛物线上,点
在(1)中抛物线上,点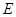 为抛物线上一动点,在
为抛物线上一动点,在 轴上是否存在点
轴上是否存在点 ,使以
,使以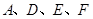 为顶点的四边形是平行四边形,如果存在,直接写出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,直接写出所有满足条件的点 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
查看答案和解析>>
科目: 来源:2012届福建省永春县九年级上学期期末数学试卷(带解析) 题型:解答题
已知抛物线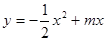 过点(8,0),
过点(8,0),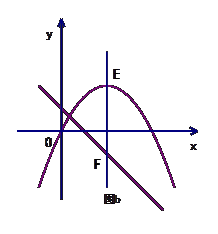
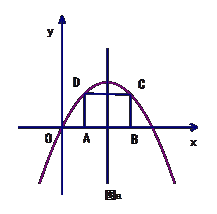
(1)求 的值;
的值;
(2)如图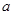 ,在抛物线内作矩形ABCD,使点C、D落在抛物线上,点A、B落在
,在抛物线内作矩形ABCD,使点C、D落在抛物线上,点A、B落在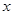 轴上,设矩形ABCD的周长为L,求L的最大值;
轴上,设矩形ABCD的周长为L,求L的最大值;
(3)如图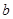 ,抛物线的顶点为E,对称轴与直线
,抛物线的顶点为E,对称轴与直线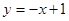 交于点F.将直线EF向右平移
交于点F.将直线EF向右平移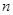 个单位后(
个单位后(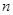 >0),交直线
>0),交直线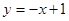 于点M,交抛物线于点N,若以E、F、M、N为顶点的四边形是平行四边形,求
于点M,交抛物线于点N,若以E、F、M、N为顶点的四边形是平行四边形,求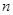 的值.
的值.
查看答案和解析>>
科目: 来源:2012届福建省永春县九年级上学期期末数学试卷(带解析) 题型:解答题
已知二次函数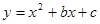 的图象经过A(2,0)、B(0,-6)两点.
的图象经过A(2,0)、B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)求该二次函数图象与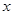 轴的另一个交点.
轴的另一个交点.
查看答案和解析>>
科目: 来源:2012届浙江省富阳市永兴中学九年级上学期第二次知识检测数学试卷(带解析) 题型:解答题
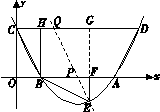
如图,抛物线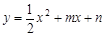 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
求(1)求C点的坐标及抛物线的解析式;
(2)将△BCH绕点B按顺时针旋转90°后 再沿x轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
(3)设过点E的直线交AB边于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由. 
查看答案和解析>>
科目: 来源:2012届浙江省富阳市永兴中学九年级上学期第二次知识检测数学试卷(带解析) 题型:解答题
春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏现象称为霜冻灾害.某种植物在气温是0℃以下持续时间超过3小时,即遭到霜冻灾害,需采取预防措施.下图是气象台某天发布的该地区气象信息,预报了次日0时至8时气温随着时间变化情况,其中0时至5时的图象满足一次函数关系,5时至8时的图象满足函数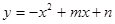 .请根据图中信息,解答下列问题:
.请根据图中信息,解答下列问题:
(1)求次日5时的气温.
(2)求二次函数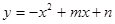 的解析式.
的解析式.
(3)判断次日是否需要采取防霜措施,并说明理由.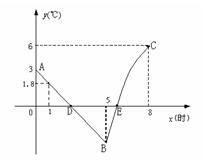
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com