
科目: 来源:2011届河北省蠡县中考模拟考试数学试卷(带解析) 题型:解答题
已知二次函数的图象经过点(0,3),(-3,0),(2, -5),且与x轴交于A、B两点.
(1)试确定此二次函数的解析式;
(2)求出抛物线的顶点C的坐标;
(3)判断点P(-2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(黑龙江龙东地区卷)数学(带解析) 题型:解答题
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0)。
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且 ,求点B的坐标。
,求点B的坐标。
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(黑龙江黑河齐齐哈尔大兴安岭鸡西卷)数学(带解析) 题型:解答题
如图,抛物线 与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式.
(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.
注:二次函数 (
( ≠0)的对称轴是直线
≠0)的对称轴是直线 =
=

查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(黑龙江哈尔滨卷)数学(带解析) 题型:解答题
小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40 cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,这个三角形面积S最大?最大面积是多少?
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(黑龙江大庆卷)数学(带解析) 题型:解答题
将一根长为16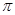 厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为
厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为 和
和 .
.
(1)求 与
与 的关系式,并写出
的关系式,并写出 的取值范围;
的取值范围;
(2)将两圆的面积和S表示成 的函数关系式,求S的最小值.
的函数关系式,求S的最小值.
查看答案和解析>>
科目: 来源:2012届山东邹城北宿中学九年级3月月考数学试卷(带解析) 题型:解答题
已知抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)若点D(m,m+1)在第一象限的抛物线上, 求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连结BD,若点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目: 来源:2010—2011学年山东省莒南八中九年级上册数学试卷(带解析) 题型:解答题
我县某工艺厂为配合60年国庆,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价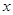 (元∕件) (元∕件) | …… | 30 | 40 | 50 | 60 | …… |
每天销售量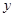 (件) (件) | …… | 500 | 400 | 300 | 200 | …… |
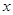 、
、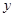 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想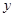 与
与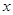 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式; 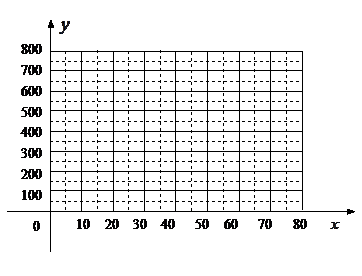
查看答案和解析>>
科目: 来源:2010—2011学年山东省莒南八中九年级上册数学试卷(带解析) 题型:解答题
如图,已知二次函数 的图像经过点A(-3,-1)和点B(-3,-9).
的图像经过点A(-3,-1)和点B(-3,-9).
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,-m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
查看答案和解析>>
科目: 来源:2010—2011学年江苏镇江市九年级上期末学情分析数学试卷(带解析) 题型:解答题
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究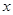 轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2010—2011学年江苏镇江市九年级上期末学情分析数学试卷(带解析) 题型:解答题
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: .
.
(1)设李明每月获得利润为W(元),当销售单价定为多少元时,每月可获得最大利润?(不需求出利润的最大值)
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com