
科目: 来源:2012届江苏省兴化市楚水初级中学九年级中考模拟数学试卷(带解析) 题型:解答题
已知,如图,A,B分别在x轴和y轴上,且OA=2OB,直线y1=kx+b经过A点与抛物线y2=-x2+2x+3交于B,C两点,
(1)试求k,b的值及C点坐标;
(2)x取何值时y1,y2均随x的增大而增大;
(3)x取何值时y1>y2.
查看答案和解析>>
科目: 来源:2012届江苏省兴化市楚水初级中学九年级中考模拟数学试卷(带解析) 题型:解答题
泰州新星电子科技公司积极应对世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线 的一部分,且点A,B,C的横坐标分别为4,10,12
的一部分,且点A,B,C的横坐标分别为4,10,12
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程);
(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?
查看答案和解析>>
科目: 来源:2009年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
如图,抛物线 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.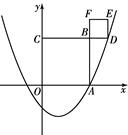
(1)求a的值.
(2)求点F的坐标.
查看答案和解析>>
科目: 来源:2008年初中毕业升学考试(浙江温州卷)数学(带解析) 题型:解答题
一次函数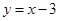 的图象与
的图象与 轴,
轴, 轴分别交于点
轴分别交于点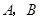 .一个二次函数
.一个二次函数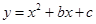 的图象经过点
的图象经过点 .
.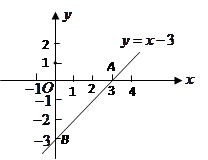
(1)求点 的坐标,并画出一次函数
的坐标,并画出一次函数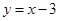 的图象;
的图象;
(2)求二次函数的解析式及它的最小值.
查看答案和解析>>
科目: 来源:2006年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
如图①,正方形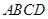 的顶点
的顶点 的坐标分别为
的坐标分别为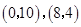 ,顶点
,顶点 在第一象限.点
在第一象限.点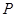 从点
从点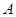 出发,沿正方形按逆时针方向匀速运动,同时,点
出发,沿正方形按逆时针方向匀速运动,同时,点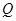 从点
从点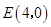 出发,沿
出发,沿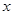 轴正方向以相同速度运动.当点
轴正方向以相同速度运动.当点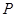 到达点
到达点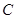 时,
时,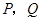 两点同时停止运动,设运动的时间为
两点同时停止运动,设运动的时间为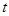 秒.
秒.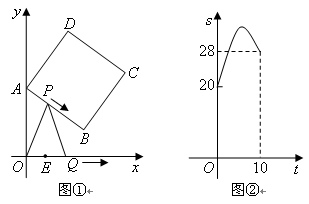
(1)求正方形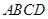 的边长.(2分)
的边长.(2分)
(2)当点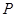 在
在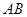 边上运动时,
边上运动时,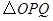 的面积
的面积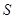 (平方单位)与时间
(平方单位)与时间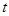 (秒)之间的函数图象为抛物线的一部分(如图②所示),求
(秒)之间的函数图象为抛物线的一部分(如图②所示),求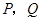 两点的运动速度.(2分)
两点的运动速度.(2分)
(3)求(2)中面积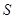 (平方单位)与时间
(平方单位)与时间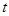 (秒)的函数关系式及面积
(秒)的函数关系式及面积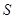 取最大值时点
取最大值时点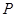 的坐标.(4分)
的坐标.(4分)
(4)若点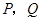 保持(2)中的速度不变,则点
保持(2)中的速度不变,则点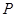 沿着
沿着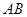 边运动时,
边运动时,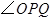 的大小随着时间
的大小随着时间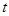 的增大而增大;沿着
的增大而增大;沿着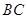 边运动时,
边运动时,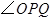 的大小随着时间
的大小随着时间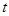 的增大而减小.当点
的增大而减小.当点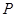 沿着这两边运动时,使
沿着这两边运动时,使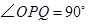 的点
的点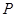 有 个.(2分)
有 个.(2分)
(抛物线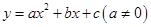 的顶点坐标是
的顶点坐标是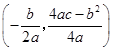 .)
.)
查看答案和解析>>
科目: 来源:2006年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
如图,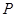 为抛物线
为抛物线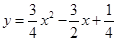 上对称轴右侧的一点,且点
上对称轴右侧的一点,且点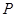 在
在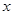 轴上方,过点
轴上方,过点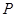 作
作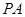 垂直
垂直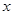 轴于点
轴于点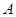 ,
,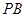 垂直
垂直 轴于点
轴于点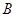 ,得到矩形
,得到矩形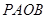 .若
.若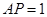 ,求矩形
,求矩形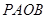 的面积.
的面积.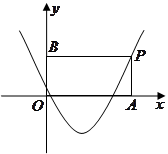
查看答案和解析>>
科目: 来源:2005年初中毕业升学考试(浙江台州卷)数学(带解析) 题型:解答题
如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.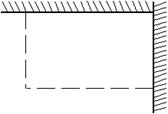
(1)设矩形的一边为 (m),面积为
(m),面积为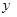 (m2),求
(m2),求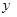 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)当 为何值时,所围苗圃的面积最大,最大面积是多少?
为何值时,所围苗圃的面积最大,最大面积是多少?
查看答案和解析>>
科目: 来源:2004年初中毕业升学考试(浙江温州卷)数学(带解析) 题型:解答题
已知抛物线y=-x2+2(m-3)x+m-1与x轴交于B,A两点,其中点B在x轴的负半轴上,点A在x轴的正半轴上,该抛物线与y轴于点C。
(1)写出抛物线的开口方向与点C的坐标(用含m的式子表示);(2分)
(2)若tg∠CBA=3,试求抛物线的解析式;(6分)
(3)设点P(x,y)(其中0<x<3)是(2)中抛物线上的一个动点,试求四边形AOCP的面积的最大值及此时点P的坐标。(6分)
查看答案和解析>>
科目: 来源:2012届重庆一中初三6月第二次定时作业数学试题(带解析) 题型:解答题
如图 ,梯形
,梯形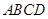 中,
中,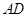 ∥
∥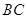 ,
,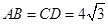 ,
,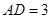 ,
,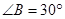 .动点
.动点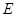 从点
从点 出发,以每秒
出发,以每秒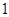 个单位长度的速度在线段
个单位长度的速度在线段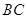 上运动;动点
上运动;动点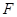 同时从点
同时从点 出发,以每秒
出发,以每秒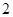 个单位长度的速度在线段
个单位长度的速度在线段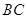 上运动.以
上运动.以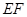 为边作等边△
为边作等边△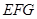 ,与梯形
,与梯形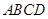 在线段
在线段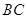 的同侧.设点
的同侧.设点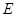 、
、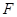 运动时间为
运动时间为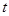 ,当点
,当点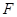 到达
到达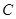 点时,运动结束.
点时,运动结束.
(1)当等边△ 的边
的边 恰好经过点
恰好经过点 时,求运动时间
时,求运动时间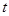 的值;
的值;
(2)在整个运动过程中,设等边△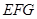 与梯形
与梯形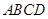 的重合部分面积为
的重合部分面积为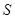 ,请直接写出
,请直接写出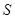 与
与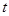 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量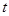 的取值范围;
的取值范围;
(3)如图 ,当点
,当点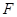 到达
到达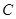 点时,将等边△
点时,将等边△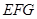 绕点
绕点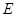 旋转
旋转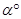 (
(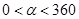 ),
),
直线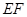 分别与直线
分别与直线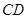 、直线
、直线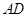 交于点
交于点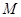 、
、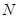 .是否存在这样的
.是否存在这样的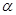 ,使△
,使△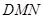 为等腰三角形?若存在,请求出此时线段
为等腰三角形?若存在,请求出此时线段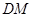 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2010届江苏省扬州市梅岭中学九年级第一次模拟考试数学试卷(带解析) 题型:解答题
如图,直线 分别交
分别交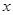 轴,
轴,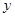 轴于
轴于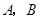 两点,以
两点,以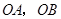 为边作矩形
为边作矩形 ,
,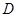 为
为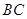 的中点.以
的中点.以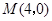 ,
,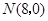 为斜边端点作等腰直角三角形
为斜边端点作等腰直角三角形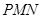 ,点
,点 在第一象限,设矩形
在第一象限,设矩形 与
与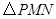 重叠部分的面积为
重叠部分的面积为 .
.
(1)求点 的坐标;
的坐标;
(2)当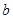 值由小到大变化时,求
值由小到大变化时,求 与
与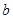 的函数关系式;
的函数关系式;
(3)若在直线 上存在点
上存在点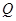 ,使
,使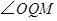 等于
等于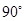 ,求出
,求出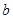 的取值范围;
的取值范围;
(4)在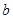 值的变化过程中,若
值的变化过程中,若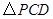 为等腰三角形,请直接写出所有符合条件的
为等腰三角形,请直接写出所有符合条件的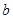 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com