
科目: 来源:2013届江苏无锡新领航教育咨询有限公司九年级暑假上课验收数学试卷(带解析) 题型:解答题
小明在一次高尔夫球比赛中,从山坡下的O点打出一记球向山坡上的球洞A点飞去,球的飞行路线为抛物线. 如果不考虑空气阻力,当球飞行的水平距离为9米时,球达到最大水平高度为12米.已知山坡OA与水平方向的夹角为30o,O、A两点相距  米.请利用下面所给的平面直角坐标系探索下列问题:
米.请利用下面所给的平面直角坐标系探索下列问题:
(1)求出点A的坐标;
(2)判断小明这一杆能否把高尔夫球从O点直接打入球洞A点,并说明理由.
查看答案和解析>>
科目: 来源:2012届安徽马鞍山金瑞初级中学九年级中考模拟(一)数学试卷(带解析) 题型:解答题
如图,抛物线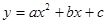 经过点O(0,0),A(4,0),B(5,5),点C是y轴负半轴上一点,直线
经过点O(0,0),A(4,0),B(5,5),点C是y轴负半轴上一点,直线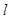 经过B,C两点,且
经过B,C两点,且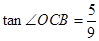 .
.
(1)求抛物线的解析式;
(2)求直线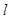 的解析式;
的解析式;
(3) 过O,B两点作直线,如果P是直线OB上的一个动点,过点P作直线PQ平行于y轴,交抛物线于点Q。问:是否存在点P,使得以P,Q,B为顶点的三角形与△OBC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由。
查看答案和解析>>
科目: 来源:2012届安徽马鞍山含山一中九年级第二学期数学月考试卷(带解析) 题型:解答题
2011年长江中下游地区发生了特大旱情,为抗旱保丰收,某地政府制定了农户投资购买抗旱设备的补贴办法,其中购买Ⅰ型、Ⅱ型抗旱设备所投资的金额与政府补贴的额度存在下表所示的函数对应关系.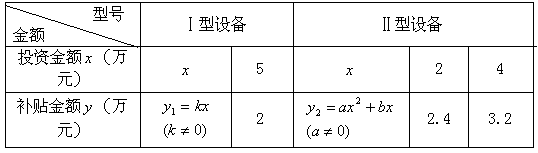
(1)分别求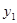 和
和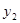 的函数解析式;
的函数解析式;
(2)有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买,请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
查看答案和解析>>
科目: 来源:2012届安徽淮南洞山中学九年级第四次教学质量检测数学试卷(带解析) 题型:解答题
如图,已知二次函数y=ax2+bx+c的图象经过A(1,0)、B(5,0)、C(0,5)三点。
(1)求这个二次函数的解析式;
(2)过点C的直线y=kx+b与这个二次函数的图象相交于点E(4,m),请求出△CBE的面积S的值。
查看答案和解析>>
科目: 来源:2012届安徽淮南洞山中学九年级第四次教学质量检测数学试卷(带解析) 题型:解答题
已知抛物线y=ax2+4ax+m(a≠0)与x轴的交点为A(-1,0),B(x2,0)。
(1)直接写出一元二次方程ax2+4ax+m=0的两个根:x1 = , x2 =
(2)原抛物线与y轴交于C点,CD∥x轴交抛物线于D点,求CD的值;
(3)若点E(1,y1),点F(-3,y2)在原抛物线上,你能比较出y2和y1; 的大小吗?若能,请比较出大小,若不能,请说明理由。
查看答案和解析>>
科目: 来源:2012届重庆巴蜀中学九年级中考第五次6月考试押题数学试卷(带解析) 题型:解答题
如图,在梯形纸片ABCD中,BC∥AD,∠A+∠D=90°,tanA=2,过点B作BH⊥AD与H,BC=BH=2.动点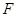 从点
从点 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿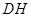 运动到点
运动到点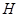 停止,在运动过程中,过点
停止,在运动过程中,过点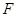 作
作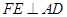 交折线
交折线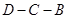 于点
于点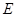 ,将纸片沿直线
,将纸片沿直线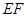 折叠,点
折叠,点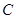 、
、 的对应点分别是点
的对应点分别是点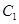 、
、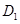 。设
。设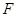 点运动的时间是
点运动的时间是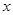 秒(
秒(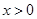 )。
)。
(1)当点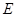 和点
和点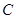 重合时,求运动时间
重合时,求运动时间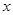 的值;
的值;
(2)在整个运动过程中,设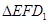 或四边形
或四边形 与梯形
与梯形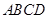 重叠部分面积为
重叠部分面积为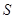 ,请直接写出
,请直接写出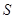 与
与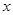 之间的函数关系式和相应自变量
之间的函数关系式和相应自变量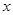 的取值范围;
的取值范围;
(3)平移线段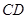 ,交线段
,交线段 于点
于点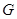 ,交线段
,交线段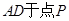 。在直线
。在直线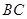 上存在点
上存在点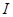 ,使
,使 为等腰直角三角形。请求出线段
为等腰直角三角形。请求出线段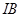 的所有可能的长度。
的所有可能的长度。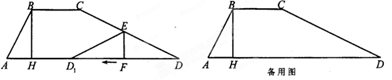
查看答案和解析>>
科目: 来源:2012届重庆巴蜀中学九年级中考第五次6月考试押题数学试卷(带解析) 题型:解答题
2012年3月23日至3月25日为期3天、以“云联世界感知未来”为主题的2012中国(重庆)国际云计算博览会(下称云博会)在渝召开,重庆新市委书记张德江说在未来10年内重庆实施“云端计划” 建设智慧重庆。 市委市政府非常重视“云端服务器”的建设,几年前就已经着手建设“云端服务器”,据统计,某行政区在去年前7个月内,“云端服务器”的数量与月份之间的关系如下表:
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
云端服务器数量 (台) (台) | 32 | 34 | 36 | 38 | 40 | 42 | 44 |
 (台)与月份x(月)之间存在如图所示的变化趋势:
(台)与月份x(月)之间存在如图所示的变化趋势:
 与x之间的函数关系式,根据如图所示的变化趋势,直接写出
与x之间的函数关系式,根据如图所示的变化趋势,直接写出 与x之间满足的一次函数关系式;
与x之间满足的一次函数关系式; (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式:  ,(1≤x≤7,且x为整数);8至12月份的资金投入
,(1≤x≤7,且x为整数);8至12月份的资金投入 (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式: (8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;
(8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;查看答案和解析>>
科目: 来源:2012届重庆巴蜀中学九年级中考第五次6月考试押题数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,二次函数 经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m,
经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m, ),点C是抛物线在第三象限的一点,且横坐标为-2.
),点C是抛物线在第三象限的一点,且横坐标为-2.
(1)求抛物线的解析式和直线BC的解析式。
(2)直线BC与 x轴相交于点D,求△OBC的面积
查看答案和解析>>
科目: 来源:2012届重庆八中九年级3月月考数学试卷(带解析) 题型:解答题
如图,梯形ABCD中,BC∥AD,∠ABC=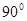 ,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
(1)求PQ经过O 点时的运动时间t;
(2)求s与t的函数关系式,并求s的最大值;
(3)如图(2),若AB的中点为H,DK=1,过H作HT∥AD,交BD于T,交BK于G,求G在正方形PQMN内部时t的取值范围。
查看答案和解析>>
科目: 来源:2012届重庆八中九年级3月月考数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系xOy中,二次函数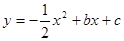 的图象经过A(2,0)B(0,-6)两点
的图象经过A(2,0)B(0,-6)两点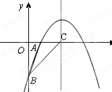
(1)求该二次函数的解析式
(2)设该二次函数的对称轴与 轴交于点C,连结BA、BC,求△ABC的面积
轴交于点C,连结BA、BC,求△ABC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com