
科目: 来源:2012年初中毕业升学考试(福建龙岩卷)数学(带解析) 题型:解答题
在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边 AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物
线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段
AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
如图,在平面直角坐标系中,直线y=-2x+42交x轴与点A,交直线y=x于点B,抛物线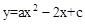 分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上.
分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上.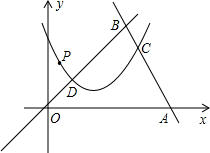
(1)求点C、D的纵坐标.
(2)求a、c的值.
(3)若Q为线段OB上一点,且P、Q两点的纵坐标都为5,求线段PQ的长.
(4)若Q为线段OB或线段AB上的一点,PQ⊥x轴,设P、Q两点之间的距离为d(d>0),点Q的横坐标为m,直接写出d随m的增大而减小时m的取值范围.
(参考公式:二次函数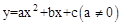 图像的顶点坐标为
图像的顶点坐标为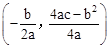 )
)
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖北襄阳卷)数学(带解析) 题型:解答题
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.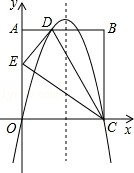
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(湖北恩施卷)数学(带解析) 题型:解答题
如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(广西来宾卷)数学(带解析) 题型:解答题
已知抛物线y=ax2+2x+c的图象与x轴交于点A(3,0)和点C,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上找一点D,使得点D到点B、C的距离之和最小,并求出点D的坐标;
(3)在第一象限的抛物线上,是否存在一点P,使得△ABP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(广西北海卷)数学(带解析) 题型:解答题
大润发超市进了一批成本为8元/个的文具盒。调查发现:这种文具盒每个星期
的销售量y(个)与它的定价x(元/个)的关系如图所示: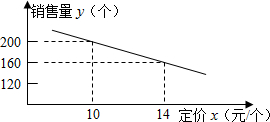
(1)求这种文具盒每个星期的销售量y(个)与它的定价x(元/个)之间的函数关系式(不必写出自变
量x的取值范围);
(2)每个文具盒定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润最高?
最高利润是多少?
查看答案和解析>>
科目: 来源:2012届重庆全善学校九年级下学期第二次月考数学试卷(带解析) 题型:解答题
如图1,在Rt△AOB中,∠AOB=90°,AO=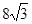 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒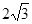 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
(1)求当等边△PMN的顶点M运动到与点O重合时t的值.
(2)求等边△PMN的边长(用t的代数式表示);
(3)如果取OB的中点D,以OD为边在Rt△AOB 内部作如图2所示的矩形ODCE,点C在线段AB上.设等边△PMN和矩形ODCE重叠部分的面积为S,请求出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
(4)在(3)中,设PN与EC的交点为R,是否存在点R,使△ODR是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届重庆全善学校九年级下学期第二次月考数学试卷(带解析) 题型:解答题
巴南区为了贯彻落实“森林重庆”,深入开展“绿化长江—重庆行动”。现决定对本区培育种植树苗的农民实施政府补贴,规定每种植一亩树苗一次性补贴农民若干元,随着补贴数额的不断增大,生产规模也不断增加,但每亩树苗的收益会相应降低。经调查,种植亩数y(亩)、每亩树苗的收益z(元)与补贴树额x(元)之间的一次函数关系如下表: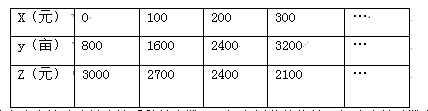
(1)分别求出政府补贴政策实施后种植亩数y、每亩树苗的收益z与政府补贴数额x之间的函数关系式;
(2)要使我区种植树苗的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值和此时种植的亩数;(总收益=种植亩数 每亩树苗的收益)
每亩树苗的收益)
(3)在取得最大收益的情况下,经市场调查,培育种植水果类树苗经济效益更好,今年该地区决定用种植树苗总面积m﹪的土地种植水果类树苗,因环境和经济等因素的制约,种植水果类树苗的面积不超过300亩 .经测算,种植水果类树苗需用的支架、塑料膜等材料每亩费用为2700元,此外还需购置喷灌设备,这项费用(元)与种植水果类树苗面积(亩)的平方成正比例,比例系数为9.预计今年种植水果类树苗后的这部分土地的收益比没种植前的收益每亩增加了7500元,这样,该地区今年因种植水果类树苗而增加的收益(扣除材料费和设备费后)共570000元.求m的值.
(结果精确到个位,参考数据: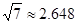 ,
,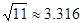 )
)
查看答案和解析>>
科目: 来源:2012届山西省临汾市平阳中学九年级下学期第一次月考试卷(带解析) 题型:解答题
如图, 已知抛物线 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为以AC为腰的等腰三角形,若存在,求点P的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源:2013届江苏无锡新领航教育咨询有限公司九年级暑假上课验收数学试卷(带解析) 题型:解答题
如图10,在平面直角坐标系中,正方形OABC边长是4,点A、C分别在y轴、x轴的正半轴上.动点P从点A开始,以每秒2个单位长度的速度在线段AB上来回运动.动点Q从点B开始沿B→C→O的方向,以每秒1个单位长度的速度向点O运动.P、Q两点同时出发,当点Q到达点O时,P、Q两点同时停止运动.设运动时间为t,△OPQ的面积为S.
(1)当t =1时,S = ;
(2)当0≤ t ≤ 2时,求满足△BPQ的面积有最大值的P、Q两点坐标;
(3)在P、Q两点运动的过程中,是否存在某一时刻,使得S = 6.若存在,请直接写出所有符合条件的P点坐标;若不存在,请说明理由.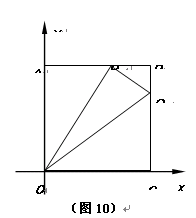
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com