已知二次函数y=-x²+4x+5，完成下列各题：
（1）将函数关系式用配方法化为的形式，并写出它的顶点坐标、对称轴.
（2）求出它的图象与坐标轴的交点坐标.
（3）在直角坐标系中，画出它的图象.

（4）根据图象说明：当x为何值时，y>0；当x为何值时，y<0.

如图，某学生推铅球，铅球出手（点A处）的高度是0.6m，出手后的铅球沿一段抛物线运行，当运行到最高3m时，水平距离x＝4m.　
(1)求这个二次函数的解析式； (2)该男同学把铅球推出去多远？

某水果批发商场经销一种水果，如果每千克盈利10元，每天可售出500千克.经市场调查发现， 在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克.
（1）当每千克涨价为多少元时，每天的盈利最多？最多是多少？
（2）若商场只要求保证每天的盈利为6000元，同时又可使顾客得到实惠，每千克应涨价为多少元？

如图，隧道的横截面由抛物线和长方形构成，长方形的长是8m，宽是2m，抛物线的解析式为。
（1）一辆货运车车高4m，宽2m，它能通过该隧道吗？
（2）如果该隧道内设双行道，中间遇车间隙为0.4m，那么这辆卡车是否可以通过？

求证：m取任何实数时，抛物线的图象与x轴必有两个交点．

已知二次函数y=x²-5x-6．
(1)求此函数图象的顶点A和其与x轴的交点B和C的坐标；
(2)求△ABC的面积．

已知抛物线与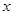交于A(－1，0)、B(3，0)两点，与轴交于点C(0，3)，求抛物线的解析式；

已知，如图所示抛物线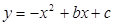与x的两个交点分别为A（1，0），B（3，0）。

（1）求抛物线的解析式；
（2）设点P在该抛物线上滑动,且满足条件S_△PAB = 1这样的点P有几个?并求出所有点P 的坐标；
（3）设抛物线交y轴于点C，问该抛物线对称轴上是否存在点M，使得△MAC的周长最小．若存在，求出点M的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M、N，直线m运动的时间为t（秒）．
（1）点A的坐标是：_________，点C的坐标是：__________；
（2）设△OMN的面积为S，求S与t的函数关系式；
（3）探求（2）中得到的函数S有没有最大值？若有，求出最大值；若没有，说明理由．

已知，如图，在平面直角坐标系中，点A坐标为(－2，0)，点B坐标为 （0，2 ），点E为线段AB上的动点(点E不与点A，B重合)，以E为顶点作∠OET=45°，射线ET交线段OB于点F，C为y轴正半轴上一点，且OC=AB，抛物线y=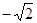x²+mx+n的图象经过A，C两点.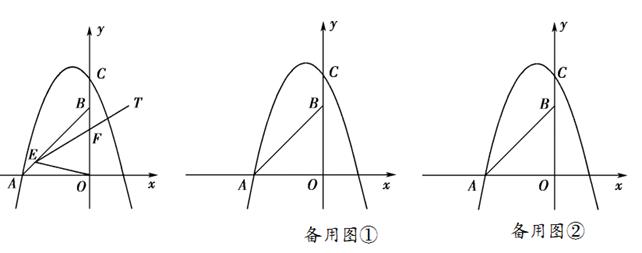

（1） 求此抛物线的函数表达式；
（2） 求证：∠BEF=∠AOE；
（3） 当△EOF为等腰三角形时，求此时点E的坐标；
（4） 在（3）的条件下，当直线EF交x轴于点D，P为（1） 中抛物线上一动点，直线PE交x轴于点G，在直线EF上方的抛物线上是否存在一点P，使得△EPF的面积是△EDG面积的（） 倍.若存在，请直接写出点P的坐标；若不存在，请说明理由．
温馨提示：考生可以根据题意，在备用图中补充图形，以便作答.