
科目: 来源:2013届浙江临安於潜第一初级中学九年级10月单元练习数学试卷(带解析) 题型:解答题
已知二次函数当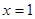 时,
时, 有最大值为5,且它的图象经过点(2,3),求:
有最大值为5,且它的图象经过点(2,3),求:
(1)这个函数的关系式;
(2)当函数值 不小于3时,请直接写出对应的自变量
不小于3时,请直接写出对应的自变量 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2013届浙江温州育英学校九年级10月月考数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交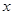 轴于A、B两点,开口向下的抛物线经过点A、B,且其顶点
轴于A、B两点,开口向下的抛物线经过点A、B,且其顶点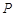 在⊙C上.
在⊙C上.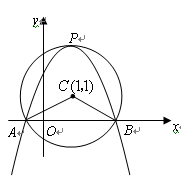
(1)求出A、B两点的坐标;(5分)
(2)试确定此抛物线的解析式;(5分)
(3)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.(4分)
查看答案和解析>>
科目: 来源:2013届浙江温州育英学校九年级10月月考数学试卷(带解析) 题型:解答题
某商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件。设这种商品的销售单价为x元,商品每天销售这种商品所获得的利润为y元.
(1)给定x的一些值,请计算y的一些值.(每空1分,共4分)
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | 320 | | | | | … |
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | 320 | 420 | 480 | 500 | 480 | … |
查看答案和解析>>
科目: 来源:2013届浙江温州育英学校九年级10月月考数学试卷(带解析) 题型:解答题
如图,已知二次函数 的图象经过A(2,0)、B(0,―6)两点.
的图象经过A(2,0)、B(0,―6)两点.
(1)求这个二次函数的解析式.(6分)
(2)设该二次函数的对称轴与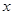 轴交于点C,连结BA、BC,求△ABC的面积.(6分)
轴交于点C,连结BA、BC,求△ABC的面积.(6分)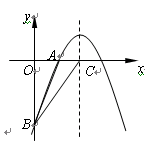
查看答案和解析>>
科目: 来源:2013届浙江温州育英学校九年级10月月考数学试卷(带解析) 题型:解答题
已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
(1)求a和k的值;(4分)
(2)反比例函数的图象是否经过二次函数图象的顶点,为什么?(4分)
查看答案和解析>>
科目: 来源:2012届浙江湖州环渚学校九年级中考三模数学试卷(带解析) 题型:解答题
如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.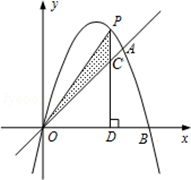
(1)求出二次函数的解析式;
(2)当点P在直线OA的上方时,用含m的代数式表示线段PC的长,并求线段PC的最大值;
(3)当m>0时,探索是否存在点P,使得△PCO为等腰三角形,如果存在,请直接写出所有P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届浙江湖州环渚学校九年级中考三模数学试卷(带解析) 题型:解答题
如图1,抛物线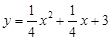 与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.
与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.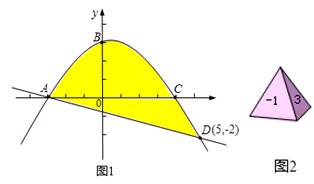
(1)求A、C两点坐标和直线AD的解析式;
(2)如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点P(m,n)落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
查看答案和解析>>
科目: 来源:2012-2013学年河北邢台第二中学初三第一学期第一次月数学试卷(带解析) 题型:解答题
已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,-8),对称轴为x=4.
(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点Q的运动速度;若不存在,请说明理由;
(3)在(2)的结论下,直线x=1上是否存在点M使△MPQ为等腰三角形?若存在,请求出所有点M的坐标,若不存在,请说明理由.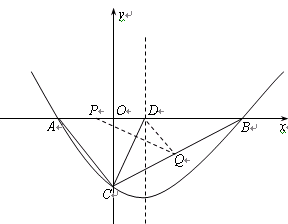
查看答案和解析>>
科目: 来源:2013届安徽省定远中学九年级第一次素质考试数学试卷(带解析) 题型:解答题
如图,抛物线y=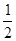 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).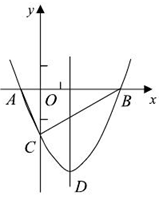
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
查看答案和解析>>
科目: 来源:2013届安徽省定远中学九年级第一次素质考试数学试卷(带解析) 题型:解答题
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.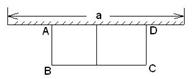
(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com