
科目: 来源:2013届浙江省杭州市亭趾实验学校九年级上期中考试数学试卷(带解析) 题型:解答题
(本小题6分)
已知一抛物线与x轴的交点是 、B(1,0),且经过点C(2,8)。
、B(1,0),且经过点C(2,8)。
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标。
查看答案和解析>>
科目: 来源:2013届浙江省杭州市亭趾实验学校九年级上期中考试数学试卷(带解析) 题型:解答题
(本小题满分6分) 已知 与
与 成反比例,
成反比例, 与
与 成正比例,并且当
成正比例,并且当 =3时,
=3时, =5,当
=5,当 =1时,
=1时, =-1;求
=-1;求 与
与 之间的函数关系式。
之间的函数关系式。
查看答案和解析>>
科目: 来源:2013届浙江省桐乡三中九年级上学期期中考试数学试卷(带解析) 题型:解答题
如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣5上.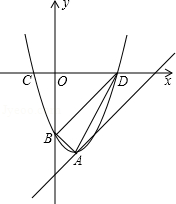
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C.D(C点在D点的左侧),试判断△ABD的形状;
(3)是否存在一点P,使以点P、A.B.D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013届浙江省桐乡三中九年级上学期期中考试数学试卷(带解析) 题型:解答题
某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每 辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出x辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)
(1)公司每日租出x辆车时,每辆车的日租金为 元(用含x的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
查看答案和解析>>
科目: 来源:2013届浙江省桐乡三中九年级上学期期中考试数学试卷(带解析) 题型:解答题
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心, PC为半径的⊙P与x轴的正半轴交于A、B两点,函数y=ax²+bx+4过A,B,C三点且AB=6.
⑴求⊙P的半径R的长;
⑵若点E在y轴上,且△ACE是等腰三角形,试写出所有点E的坐标;
查看答案和解析>>
科目: 来源:2013届浙江建德李家镇初级中学九年级上期中考试数学试卷(带解析) 题型:解答题
已知直线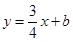 与抛物线
与抛物线 交于点A(1,
交于点A(1,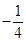 ),与
),与 轴交于点C.
轴交于点C.
(1)求抛物线的解析式和点C的坐标;
(2)把(1)中的抛物线向右平移2个单位,再向上平移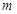 个单位(
个单位(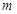 >0),抛物线与
>0),抛物线与 轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求
轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求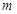 的值;
的值;
(3)如图,把抛物线向右平移2个单位,再向上平移 个单位(
个单位( >0),抛物线与
>0),抛物线与 轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时
轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.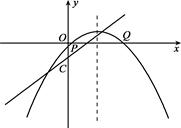
查看答案和解析>>
科目: 来源:2013届浙江建德李家镇初级中学九年级上期中考试数学试卷(带解析) 题型:解答题
已知二次函数 ,
,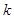 是不为0的常数.
是不为0的常数.
(1)除0以外,不论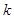 取何值时,这个二次函数的图像一定会经过两个定点,请你求出这两个定点中的其中一个;
取何值时,这个二次函数的图像一定会经过两个定点,请你求出这两个定点中的其中一个;
(2)如果该二次函数的顶点不在直线 的右侧,求
的右侧,求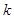 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2013届江苏省大丰市第四中学九年级12月月考数学试卷(带解析) 题型:解答题
在直角坐标系中,已知抛物线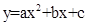 与x轴交于点A(1,0)和点B,顶点为P.
与x轴交于点A(1,0)和点B,顶点为P.
(1)若点P的坐标为(-1,4),求此时抛物线的解析式;
(2)如图若点P的坐标为(-1,k),k<0,点Q是y轴上一个动点,
当k为何值时,QB+QP取得最小值为5;
(3)试求满足(2)时动点Q的坐标. (本题12分)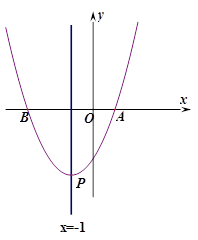
查看答案和解析>>
科目: 来源:2013届江苏省大丰市第四中学九年级12月月考数学试卷(带解析) 题型:解答题
已知:如图,矩形ABCD中,CD=2,AD=3,以C点为圆心,作一个动圆,与线段AD交于点P(P和A、D不重合),过P作⊙C的切线交线段AB于F点.
(1)求证:△CDP∽△PAF;
(2)设DP=x,AF=y,求y关于x的函数关系式,及自变量x的取值范围;
(3)是否存在这样的点P,使△APF沿PF翻折后,点A落在BC上,请说明理由.(本题12分)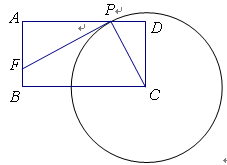
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com