
科目: 来源:2013届北京市昌平区九年级上学期期末考试数学试卷(带解析) 题型:解答题
如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为12米时,球移动的水平距离PD为9米 .已知山坡PA与水平方向PC的夹角为30o,AC⊥PC于点C, P、A两点相距 米.请你建立适当的平面直角坐标系解决下列问题.
米.请你建立适当的平面直角坐标系解决下列问题. 
(1)求水平距离PC的长;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小明这一杆能否把高尔夫球从P点直接打入球洞A.
查看答案和解析>>
科目: 来源:2013届北京市昌平区九年级上学期期末考试数学试卷(带解析) 题型:解答题
二次函数 的图象与
的图象与 轴的一个交点为A
轴的一个交点为A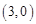 ,另一个交点为B,与
,另一个交点为B,与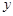 轴交于点C.
轴交于点C.
(1)求 的值及点B、点C的坐标;
的值及点B、点C的坐标;
(2)直接写出当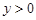 时,
时, 的取值范围;
的取值范围;
(3)直接写出当 时,
时, 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2013届北京市东城区九年级上学期期末考试数学试卷(带解析) 题型:解答题
在平面直角坐标系xOy中,抛物线 交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.
交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.
(1)求抛物线的解析式;
(2)点D是y轴正半轴上一点,且在B点上方,若∠DCB=∠CAB,请你猜想并证明CD与AC的位置关系;
(3)设与△AOB重合的△EFG从△AOB的位置出发,沿x轴负方向平移t个单位长度(0<t≤3)时,△EFG与△ABC重叠部分的面积为S,求S与t之间的函数关系式.
查看答案和解析>>
科目: 来源:2013届北京市东城区九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知,二次函数 的图象如图所示.
的图象如图所示.
(1)若二次函数的对称轴方程为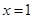 ,求二次函数的解析式;
,求二次函数的解析式;
(2)已知一次函数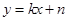 ,点
,点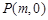 是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数
是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数 的图象于点N.若只有当1<m<
的图象于点N.若只有当1<m< 时,点M位于点N的上方,求这个一次函数的解析式;
时,点M位于点N的上方,求这个一次函数的解析式;
(3)若一元二次方程 有实数根,请你构造恰当的函数,根据图象直接写出
有实数根,请你构造恰当的函数,根据图象直接写出 的最大值.
的最大值.
查看答案和解析>>
科目: 来源:2013届北京市东城区九年级上学期期末考试数学试卷(带解析) 题型:解答题
“十八大”报告一大亮点就是关注民生问题,交通问题已经成了全社会关注的热点.为了解新建道路的通行能力,某研究表明,某种情况下,车流速度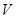 (单位:千米/时)是车流密度
(单位:千米/时)是车流密度 (单位:辆/千米)的函数,函数图象如图所示.
(单位:辆/千米)的函数,函数图象如图所示. 
(1)求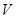 关于
关于 的函数表达式;
的函数表达式;
(2)车流量是单位时间内通过观测点的车辆数,计算公式为:车流量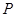 =车流速度
=车流速度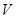 ×车流密度
×车流密度 .若车流速度
.若车流速度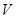 低于80千米/时,求当车流密度
低于80千米/时,求当车流密度 为多少时,车流量
为多少时,车流量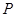 (单位:辆/时)达到最大,并求出这一最大值.
(单位:辆/时)达到最大,并求出这一最大值.
查看答案和解析>>
科目: 来源:2013届江苏省大丰市第四中学九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=CD=4,AB=7.现有M、N两点同时以相同的速度从A点出发,点M沿A—B—C-D方向前进,点N沿A—D—C-B方向前进,直到两点相遇时停止.设点M前进的路程为 ,△AMN的面积为
,△AMN的面积为 .
.
(1)试确定△AMN存在时,路程 的取值范围.
的取值范围.
(2)请你求出面积S关于路程 的函数.
的函数.
(3)当点M前进的路程为多少时,△AMN的面积最大?最大是多少?
查看答案和解析>>
科目: 来源:2013届海南洋浦中学九年级上期末考试数学试卷(带解析) 题型:解答题
如图已知二次函数图象的顶点为原点,直线 的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.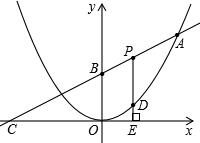
(1)求这个二次函数的解析式与B点坐标;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于D点,与x轴交于点E.设线段PD的长为h,点P的横坐标为t,求h与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,在线段AB上是否存在点P,使得以点P、D、B为顶点的三角形与△BOC相似?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012届浙江省湖州市环渚学校九年级第二次月考数学试卷(带解析) 题型:解答题
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
(1)求抛物线的解析式;
(2)已知AD=AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t 秒的移动,线段PQ被BD垂直平分,求t的值;
(3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC的值最小?若存在,请求出点M的坐标;若不存在,请说明理由。
(注:抛物线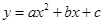 的对称轴为
的对称轴为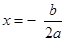 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com