
科目: 来源:2013届江苏省无锡市雪浪中学九年级12月质量监测数学试卷(带解析) 题型:解答题
分别求出对应的二次函数的解析式:
(1)已知抛物线的顶点为(-2,1),且过点(-4,3);
(2)抛物线与x轴的两个交点坐标为(-3,0)和(2,0),且它经过点(1,4).
查看答案和解析>>
科目: 来源:2013届浙江省乐清市盐盆一中九年级第一次月考数学试卷(带解析) 题型:解答题
(本题10分)如图,矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上,且OD=10,OB=8.将矩形的边BC绕点B逆时针旋转,使点C恰好与x轴上的点A重合.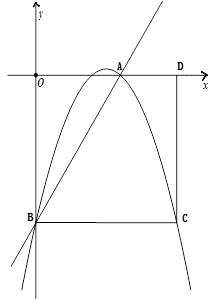
(1)直接写出点A、B的坐标:A( , )、B( , );
(2)若抛物线y=-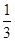 x2+bx+c经过点A、B,请求出这条抛物线的解析式;
x2+bx+c经过点A、B,请求出这条抛物线的解析式;
(3)当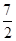 ≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
查看答案和解析>>
科目: 来源:2013届浙江省乐清市盐盆一中九年级第一次月考数学试卷(带解析) 题型:解答题
(8分) 某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施,调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目: 来源:2013届北京市怀柔区九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
(1)直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连结OP.
①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;
②试问在抛物线的对称轴上是否存在一点T,使得 的值最大.若存在,求出T点坐标;若不存在,请说明理由.
的值最大.若存在,求出T点坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013届北京市怀柔区九年级上学期期末考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,-1),交x轴于A、B两点,交y轴于点C,其中点B的坐标为(3,0).
(1)求该抛物线的解析式;
(2)设经过点C的直线与该抛物线的另一个交点为D,且直线CD和直线CA关于直线BC对称,求直线CD的解析式;
(3)在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标.
查看答案和解析>>
科目: 来源:2013届北京市怀柔区九年级上学期期末考试数学试卷(带解析) 题型:解答题
小赵投资销售一种进价为每件20元的护眼台灯.销售过程中发现,月内销售单价不变,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数 .
.
(1)设小赵每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?并求出最大利润.
(2)如果小赵想要每月获得的利润不低于2000元,那么如何制定销售单价才可以实现这一目标?
查看答案和解析>>
科目: 来源:2013届北京市怀柔区九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知反比例函数y= 的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
(1)求a的值;
(2)反比例函数的图象是否经过二次函数图象的顶点,请说明理由.
查看答案和解析>>
科目: 来源:2013届北京市顺义区九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知:如图,抛物线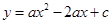 (
(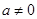 )与
)与 轴交于点
轴交于点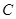 ( 0,4) ,与
( 0,4) ,与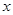 轴交于点
轴交于点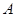 ,
,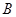 ,点
,点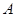 的坐标为(4,0).
的坐标为(4,0).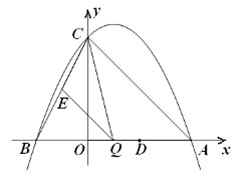
(1) 求该抛物线的解析式;
(2) 点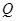 是线段
是线段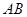 上的动点,过点
上的动点,过点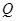 作
作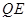 ∥
∥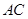 ,交
,交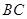 于点
于点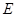 ,连接
,连接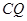 . 当
. 当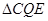 的面积最大时,求点
的面积最大时,求点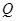 的坐标;
的坐标;
(3)若平行于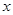 轴的动直线与该抛物线交于点
轴的动直线与该抛物线交于点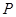 ,与直线
,与直线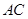 交于点
交于点 ,点
,点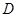 的坐标为(2,0). 问: 是否存在这样的直线,使得
的坐标为(2,0). 问: 是否存在这样的直线,使得 是等腰三角形?若存在,请求出点
是等腰三角形?若存在,请求出点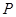 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013届北京市顺义区九年级上学期期末考试数学试卷(带解析) 题型:解答题
某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件.经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.将销售价定为多少时,才能使每天所获销售利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源:2013届浙江省杭州市运河镇亭趾实验学校九年级上学期期末考试数学试卷(带解析) 题型:解答题
如图,经过原点的抛物线 与
与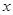 轴的另一个交点为A.过点
轴的另一个交点为A.过点 作直线
作直线 轴于点M,交抛物线于点B,过点B作直线BC∥
轴于点M,交抛物线于点B,过点B作直线BC∥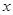 轴与抛物线交于点C(B、C不重合),连结CP.
轴与抛物线交于点C(B、C不重合),连结CP.
(1)当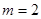 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
(2)当 时,连结CA,问
时,连结CA,问 为何值时
为何值时 ?
?
(3)过点P作 且
且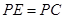 ,问是否存在
,问是否存在 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的 的值,并求出相对应的点E坐标;若不存在,请说明理由.
的值,并求出相对应的点E坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com