
科目: 来源:2013届北京市第六十三中学初三第一学期期中考试数学试卷(带解析) 题型:解答题
已知二次函数y= x2 +4x+3.
(1)用配方法将y= x2 +4x+3化成y=a (x-h) 2 +k的形式;
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)写出当x为何值时,y>0.
查看答案和解析>>
科目: 来源:2013届北京市第六十三中学初三第一学期期中考试数学试卷(带解析) 题型:解答题
已知二次函数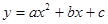 的图象与x 轴交于(2,0)、(4,0),顶点到x 轴的距离为3,求函数的解析式。
的图象与x 轴交于(2,0)、(4,0),顶点到x 轴的距离为3,求函数的解析式。
查看答案和解析>>
科目: 来源:2013届上海市松江区九年级下学期3月月考数学试卷(带解析) 题型:解答题
(本题满分12分,其中第(1)小题5分,第(2)小题4分,第(3)小题3分)
已知抛物线 过点A(-1,0),B(4,0),P(5,3),抛物线与y轴交于点C.
过点A(-1,0),B(4,0),P(5,3),抛物线与y轴交于点C.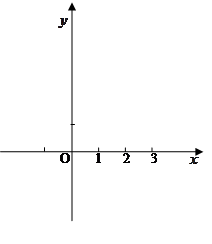
(1)求二次函数的解析式;
(2)求tan∠APC的值;
(3)在抛物线上求一点Q,过Q点作x轴的垂线,垂足为H,使得∠BQH=∠APC.
查看答案和解析>>
科目: 来源:2013届北京市门头沟区九年级上学期期末考试数学试卷(带解析) 题型:解答题
在平面直角坐标系xOy中,已知抛物线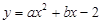 经过(2,1)和(6,-5)两点.
经过(2,1)和(6,-5)两点.
(1)求抛物线的解析式;
(2)设此抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点,点P是在直线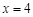 右侧的此抛物线上一点,过点P作PM
右侧的此抛物线上一点,过点P作PM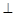
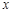 轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
(3)点E是直线BC上的一点,点F是平面内的一点,若要使以点O、B、E、F为顶点的四边形是菱形,请直接写出点F的坐标.
查看答案和解析>>
科目: 来源:2013届北京市门头沟区九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知抛物线 .
.
(1) 求证:无论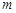 为任何实数,抛物线与
为任何实数,抛物线与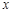 轴总有两个交点;
轴总有两个交点;
(2) 若A 、B
、B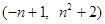 是抛物线上的两个不同点,求抛物线的解析式和
是抛物线上的两个不同点,求抛物线的解析式和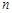 的值;
的值;
(3) 若反比例函数 的图象与(2)中的抛物线在第一象限内的交点的横坐标为
的图象与(2)中的抛物线在第一象限内的交点的横坐标为 ,且满足2<
,且满足2< <3,求k的取值范围.
<3,求k的取值范围.
查看答案和解析>>
科目: 来源:2013届北京市门头沟区九年级上学期期末考试数学试卷(带解析) 题型:解答题
如图,二次函数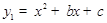 的图象与x轴交于A、B 两点,与
的图象与x轴交于A、B 两点,与 轴交于点C,且点B的坐标为(1,0),点C的坐标为
轴交于点C,且点B的坐标为(1,0),点C的坐标为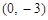 ,一次函数
,一次函数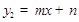 的图象过点A、C.
的图象过点A、C.
(1)求二次函数的解析式;
(2)求二次函数的图象与x轴的另一个交点A的坐标;
(3)根据图象写出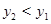 时,
时,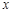 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2013届北京市门头沟区九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知二次函数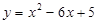 .
.
(1)将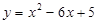 化成
化成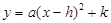 的形式;
的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当 取何值时,
取何值时,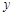 随
随 的增大而减小.
的增大而减小.
查看答案和解析>>
科目: 来源:2013届湖北省宜昌中学九年级下学期第一次月考数学试卷(带解析) 题型:解答题
(12分)已知抛物线 (
(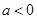 )与
)与 轴相交于点
轴相交于点 ,顶点为
,顶点为 .直线
.直线 分别与
分别与 轴,
轴, 轴相交于
轴相交于 两点,并且与直线
两点,并且与直线 相交于点
相交于点 .
.
(1)填空:试用含 的代数式分别表示点
的代数式分别表示点 与
与 的坐标,则
的坐标,则 ;
;
(2)如图,将 沿
沿 轴翻折,若点
轴翻折,若点 的对应点
的对应点 ′恰好落在抛物线上,
′恰好落在抛物线上,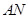 ′与
′与 轴交于点
轴交于点 ,连结
,连结 ,求
,求 的值和四边形
的值和四边形 的面积;
的面积;
(3)在抛物线 (
(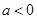 )上是否存在一点
)上是否存在一点 ,使得以
,使得以 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目: 来源:2013届湖北省黄石市第九中学九年级下学期开学联考数学试卷(带解析) 题型:解答题
平面直角坐标系xOy中,抛物线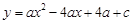 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴上的点P满足∠APB=∠ACB,求点P的坐标;
(3)在(1)的条件下,对于实数c、d,我们可用min{ c,d }表示c、d两数中较小的数,如min{3,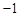 }=
}=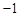 .若关于x的函数y = min{
.若关于x的函数y = min{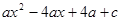 ,
,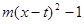
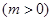 }的图象关于直线
}的图象关于直线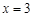 对称,试讨论其与动直线
对称,试讨论其与动直线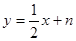 交点的个数。
交点的个数。
查看答案和解析>>
科目: 来源:2013届江苏省宿迁市四校(修远、青华中学)九年级第二次联考数学试卷(带解析) 题型:解答题
(本题满分12分)
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.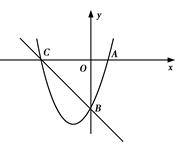
(1)求抛物线的解析式;
(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com