
科目: 来源:2013届浙江省杭州市高桥初中教育集团九年级第二学期期初质量检测数学卷(带解析) 题型:解答题
已知:如图,抛物线y=a(x-1)2+c与x轴交于点A(1-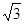 ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P'(1,3)处.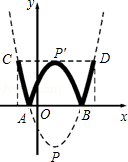
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P'作x轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比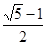 .请你计算这个“W”图案的高与宽的比到底是多少?
.请你计算这个“W”图案的高与宽的比到底是多少?
查看答案和解析>>
科目: 来源:2012-2013学年吉林省镇赉县胜利中学九年级下第三次数学模拟试题(带解析) 题型:解答题
某公司推出一种高效环保型洗涤用品,年初上市后公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)反映了该公司年初以来累积利润S(万元)与销售时间 (月)之间的关系(即前
(月)之间的关系(即前 个月的利润总和S与
个月的利润总和S与 的关系).根据图象提供的信息,解答下列问题.
的关系).根据图象提供的信息,解答下列问题.
(1)如图,已知图象上的三点坐标,求累积利润S(万元)与时间 (月)之间的函数关系式;
(月)之间的函数关系式;
(2)求截止到几月未公司累积利润可达到30万元?
(3)求第8月公司所获利润是多少元?
查看答案和解析>>
科目: 来源:2013学年吉林省镇赉县镇赉镇中学九年级下第二次综合测试数学试卷(带解析) 题型:解答题
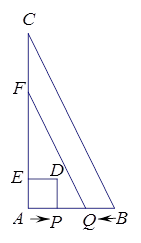
如图,ABC中,∠A=90º,AB=2㎝,AC=4㎝,动点P从点A出发,沿AB方向以1㎝/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1㎝s的速度向带你A运动,当点P到达点B时,P、Q两点同时停止运动.以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F,设点P的运动时间为t s,正方形APDE和梯形BCFQ重合部分的面积为S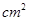 .
.
(1)当t= s时,点P与点Q重合;
(2)当t= s时,点D在QF上;
(3)当点P在Q、B两点之间(不包括Q、B两点)时,求S与t之间的函数关系式.
查看答案和解析>>
科目: 来源:2013学年吉林省镇赉县镇赉镇中学九年级下第二次综合测试数学试卷(带解析) 题型:解答题
如图,抛物线 经过点A(1,0),与
经过点A(1,0),与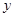 轴交于点B.
轴交于点B.
(1)求抛物线的解析式和顶点坐标;
(2)若P是坐标轴上一点,且三角形PAB是以AB为腰的等腰三角形,试求P点坐标.
查看答案和解析>>
科目: 来源:2012-2013年度江苏泰兴实验初级中学第二学期初三数学阶段试卷(带解析) 题型:解答题
已知二次函数y=-9x2-6ax-a2+2a;(1)当此抛物线经过原点,且对称轴在y轴左侧.
①求此二次函数关系式;(2分)
②设此抛物线与x轴的另一个交点为A,顶点为P,
O为坐标原点.现有一直线l:x=m随着m的
变化从点A向点O平行移动(与点O不重合),
在运动过程中,直线l与抛物线交于点Q,
求△OPQ的面积S关于m的函数关系式;(5分)
(2)若二次函数在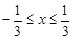 时有最大值-4,求a的值.(5分)
时有最大值-4,求a的值.(5分)
查看答案和解析>>
科目: 来源:2012-2013年度江苏泰兴实验初级中学第二学期初三数学阶段试卷(带解析) 题型:解答题
某超市经销一种销售成本为每件30元的商品.据市场调查分析,如果按每件40元
销售,一周能售出500件,若销售单价每涨1元,每周的销售量就减少10件.设销售单价为每件x元(x≥40),一周的销售量为y件.
(1)写出y与x的函数关系式(标明x的取值范围);
(2)设一周的销售利润为s元,写出s与x的函数关系式,并确定当单价在什么范围内变化时,
利润随着单价的增大而增大;
(3)在超市对该种商品投入不超过8800元的情况下,使得一周销售利润达到8000元,销售单价应定为多少?
查看答案和解析>>
科目: 来源:2013届北京市龙文教育九年级第一次中考模拟数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系xOy中,二次函数 的图象与
的图象与 轴交于
轴交于 (-1,0)、
(-1,0)、 (3,0)两点, 顶点为
(3,0)两点, 顶点为 .
.
(1) 求此二次函数解析式;
(2) 点 为点
为点 关于x轴的对称点,过点
关于x轴的对称点,过点 作直线
作直线 :
: 交BD于点E,过点
交BD于点E,过点 作直线
作直线 ∥
∥ 交直线
交直线 于
于 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
(3) 在(2)的条件下,若 、
、 分别为直线
分别为直线 和直线
和直线 上的两个动点,连结
上的两个动点,连结 、
、 、
、 ,求
,求 和的最小值.
和的最小值.
查看答案和解析>>
科目: 来源:2013届浙江省温州市育英学校九年级第二学期开学考试数学试卷(带解析) 题型:解答题
如图,坐标系上有A(2,0)、B(4,0)两点.二次函数 的图象经过这两点
的图象经过这两点
(1)求这个二次函数的解析式;
(2)设该二次函数的图象的顶点为P,抛物线向上或向下平移多少个单位,则△ABP是正三角形。
查看答案和解析>>
科目: 来源:2013届广西大学附属中学九年级上学期期末考试数学试卷(带解析) 题型:解答题
如图已知点A (-2,4) 和点B (1,0)都在抛物线 上.
上.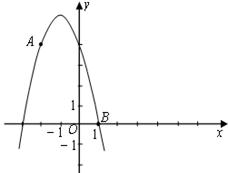
⑴求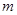 、n;
、n;
⑵向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
⑶记平移后抛物线的对称轴与直线AB′ 的交点为点C,试在 轴上找点D,使得以点B′、C、D为顶点的三角形与
轴上找点D,使得以点B′、C、D为顶点的三角形与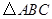 相似.
相似.
查看答案和解析>>
科目: 来源:2012-2013学年江苏阜宁第一学期期末学情调研九年级数学试卷 题型:解答题
如图,在平面直角坐标系中,已知抛物线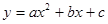 交
交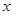 轴于
轴于 两点,交
两点,交 轴于点
轴于点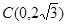 .
.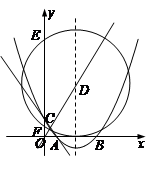
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线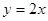 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧 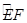 的长;
的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于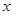 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com