
科目: 来源:2013届浙江省宁波地区第二学期九年级模拟测试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE=,EF⊥OD,垂足为F.
(1)求这个二次函数的解析式;
(2)求线段EF、OF的长(用含t的代数式表示);
(3)当△ECA为直角三角形时,求t的值.
查看答案和解析>>
科目: 来源:2012-2013学年度安徽怀远第一学期九年级期末质量检测数学试卷(带解析) 题型:解答题
如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-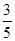 x2+3x+1的一部分,
x2+3x+1的一部分,
(1)求演员弹跳离地面的最大高度;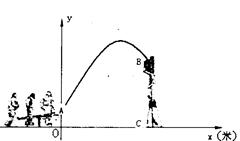 (2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这表是
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这表是
是否成功?请说明理由.
查看答案和解析>>
科目: 来源:2012-2013学年度安徽怀远第一学期九年级期末质量检测数学试卷(带解析) 题型:解答题
已知抛物线y=-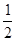 x2+x+
x2+x+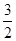
(1)该抛物线的对称轴是________,顶点坐标________;
(2)不列表在右上图的直角坐标系内描点画出该抛物线的图象,并且观察抛物线写出y <0时,x的取值范围;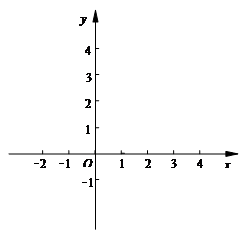
(3)请问(2)中的抛物线经过怎样平移就可以得到y=ax2的图象?
(4)若该抛物线上两点A(x1,y1)、B(x2,y2)的横坐标满足x1>x2>1,试比y1与y2的大小
查看答案和解析>>
科目: 来源:2013届江苏省无锡市新区第一实验学校九年级下学期期中考试数学试卷(带解析) 题型:解答题
已知二次函数y=ax2+bx+3的图象经过(1, )、(2,
)、(2,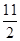 )两点,与x轴的两个交点的右边一个交点为点A,与y轴交于点B.
)两点,与x轴的两个交点的右边一个交点为点A,与y轴交于点B.
(1)求此二次函数的解析式并画出这个二次函数的图象;
(2)求线段AB的中垂线的函数解析式.
查看答案和解析>>
科目: 来源:2013届湖北省荆州市初中升学模拟考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求直线AC的解析式及B、D两点的坐标;
(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.
(3)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.
查看答案和解析>>
科目: 来源:2013届湖北省荆州市初中升学模拟考试数学试卷(带解析) 题型:解答题
已知抛物线的函数解析式为y=ax2+b x-3a(b<0),若这条抛物线经过点(0,-3),方程ax2+b x-3a=0的两根为x1,x2,且|x1-x2|=4.
⑴求抛物线的顶点坐标.
⑵已知实数x>0,请证明x+ ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+ =2.
=2.
查看答案和解析>>
科目: 来源:2013届江苏省徐州市九年级中考模拟数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,已知点 坐标为(2,4),直线
坐标为(2,4),直线 与
与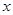 轴相交于点
轴相交于点 ,连结
,连结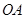 ,抛物线
,抛物线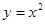 从点
从点 沿
沿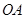 方向平移,与直线
方向平移,与直线 交于点
交于点 ,顶点
,顶点 到
到 点时停止移动.
点时停止移动.
(1)求线段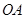 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点 的横坐标为
的横坐标为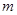 ,当
,当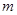 为何值时,线段
为何值时,线段 最短;
最短;
(3)当线段 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点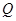 ,使△
,使△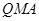 的面积与△
的面积与△ 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点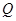 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013届江苏省徐州市九年级中考模拟数学试卷(带解析) 题型:解答题
如图所示,现有一张边长为6的正方形纸片 ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP.
(1)求证:∠APB=∠BPH;
(2)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013届江苏省徐州市九年级中考模拟数学试卷(带解析) 题型:解答题
根据对徐州市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的甲种蔬菜的销售利润y1(千元)与进货量x(吨)之间的函数 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数 的图象如图②所示.
的图象如图②所示.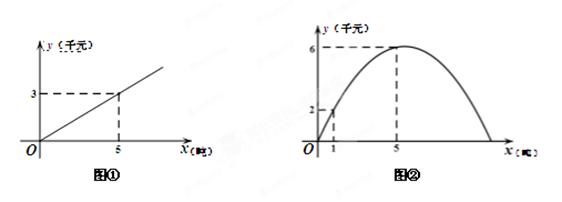
(1)分别求出y1、y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种蔬菜共10吨,设乙种蔬菜的进货量为t吨,写出这两种蔬菜所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种蔬菜各进多少吨时 获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
科目: 来源:2013届浙江省杭州市高桥初中教育集团九年级第二学期期初质量检测数学卷(带解析) 题型:解答题
【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数关系式为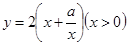
【探索研究】
(1)我们可以借鉴以前研究函数的经验,先探索函数 的图象和性质.
的图象和性质.
①填写下表,画出函数的图象;
| x | … | 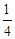 | 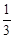 |  | 1 | 2 | 3 | 4 | … |
| y | … | | | | | | | | … |

 的最小值.
的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com