抛物线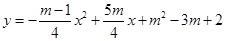与x轴的交点分别为原点O和点A，点B(2,n)在这条抛物线上．
（1）求点B的坐标；
（2）点P在线段OA上，从点O出发向点A运动，过点P作x轴的垂线，与直线OB交于点E，以PE为边在PE右侧作正方形PEDC（当点P运动时，点C、D也随之运动）．
①当正方形PEDC顶点D落在此抛物线上时，求OP的长；
②若点P从点O出发向点A作匀速运动，速度为每秒1个单位，同时线段OA上另一个点Q从点A出发向点O作匀速运动，速度为每秒2个单位（当点Q到达点O时停止运动，点P也停止运动）．过Q作x轴的垂线，与直线AB交于点F，在QF的左侧作正方形QFMN（当点Q运动时，点M、N也随之运动）．若点P运动到t秒时，两个正方形分别有一条边恰好落在同一条直线上，求此刻t的值．

某厂销售一种专利产品，现准备从专卖店销售和电视直销两种销售方案中选择一种进行销售．若只是专卖店销售，销售价格y（元/件）与月销量x（件）的函数关系式为y =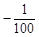x＋150，成本为40元/件，无论销售多少，每月还需支出房租费52500元，设月利润为w_专（元）（利润 = 销售额－成本－广告费）．若只是电视直销，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，40≤a≤80），当月销量为x（件）时，每月还需缴纳x² 元的广告费，设月利润为w_电（元）（利润 = 销售额－成本－附加费）．
（1）当x = 1000时，y =        元/件，w_内 =        元；
（2）分别求出w_专、w_电与x间的函数关系式（不必写x的取值范围）；
（3）当x为何值时，在专卖店销售的月利润最大？若是电视直销月利润的最大值与在专卖店销售月利润的最大值相同，求a的值；
（4）如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在专卖店还是电视直销才能使所获月利润较大？

如图，抛物线交轴于A、B两点，交轴于点C，
点P是它的顶点，点A的横坐标是3，点B的横坐标是1．

（1）求、的值；
（2）求直线PC的解析式；
（3）请探究以点A为圆心、直径为5的圆与直线PC的位置关系，并说明理由．
（参考数据，，）

某企业投资100万元引进一条农产品加工线，若不计维修、保养费用，预计投产后每年可获利33万元，该生产线投资后，从第1年到第年的维修、保养费用累计为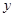（万元），且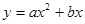，若第1年的维修、保养费用为2万元，第2年为4万元。
（1）求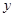与之间的关系式；
（2）投产后，这个企业在第几年就能收回投资？

已知抛物线过点A（－1，0），B（0，6），对称轴为直线x＝1
（1）求抛物线的解析式
（2）画出抛物线的草图
（3）根据图象回答：当x取何值时，y>0

若抛物线的顶点坐标是（1，16），并且抛物线与轴两交点间的距离为8，（1）试求该抛物线的关系式；
（2）求出这条抛物线上纵坐标为12的点的坐标。

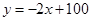某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量（万件）与销售单价（元）之间的关系可以近似地看作一次函数．（利润=售价-制造成本）
（1）写出每月的利润（万元）与销售单价（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月获得的利润为440万元？
（3）根据相关部门规定，这种电子产品的销售单价不能高于40元，如果厂商每月的制造成本不超过540万元，那么当销售单价为多少元时，厂商每月获得的利润最大？最大利润为多少万元？

已知：如图，在Rt△ABC中，∠ACB=90°，BC="3" ，tan∠BAC=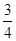，将∠ABC对折，使点C的对应点H恰好落在直线AB上，折痕交AC于点O，以点O为坐标原点，AC所在直线为x轴建立平面直角坐标系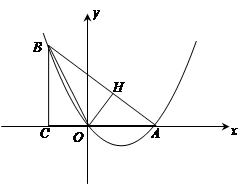

（1）求过A、B、O三点的抛物线解析式；
（2）若在线段AB上有一动点P，过P点作x轴的垂线，交抛物线于M，设PM的长度等于d，试探究d有无最大值，如果有，请求出最大值，如果没有，请说明理由．
（3）若在抛物线上有一点E，在对称轴上有一点F，且以O、A、E、F为顶点的四边形为平行四边形，试求出点E的坐标．

如图，在平面直角坐标系中，将一块等腰直角三角板ABC斜靠在两坐标轴上放在第二象限，点C的坐标为（-1，0）．B点在抛物线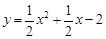的图象上，过点B作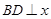轴，垂足为D，且B点横坐标为．

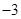（1）求证：；
（2）求BC所在直线的函数关系式；
（3）抛物线的对称轴上是否存在点P，使 △ACP是以AC为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

如图，已知△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA向点A匀速运动，同时点Q由A出发沿AC向点C匀速运动，它们的速度均为2cm/s．连接PQ，设运动的时间为t（单位：s）（0≤t≤4）．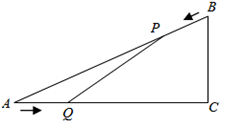

（1）当t为何值时，PQ∥BC．
（2）设△AQP的面积为S（单位：cm²），当t为何值时，S取得最大值，并求出最大值．
（3）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在，求出此时t的值；若不存在，请说明理由．