
科目: 来源:2013届四川省盐边县红格中学九年级下学期摸底考试数学试卷(带解析) 题型:解答题
如图,抛物线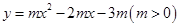 与
与 轴交于
轴交于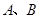 两点,与
两点,与 轴交于
轴交于 点.
点.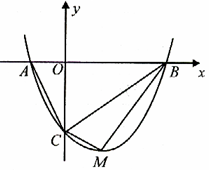
(1)请求出抛物线顶点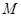 的坐标(用含
的坐标(用含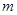 的代数式表示),
的代数式表示),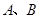 两点的坐标;
两点的坐标;
(2)经探究可知, 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;
(3)是否存在使 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013届四川省盐边县红格中学九年级下学期摸底考试数学试卷(带解析) 题型:解答题
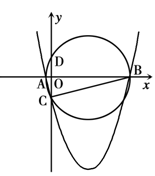
如图,已知二次函数 的图象与
的图象与 轴相交于两个不同的点
轴相交于两个不同的点 、
、 ,与
,与 轴的交点为
轴的交点为 .设
.设 的外接圆的圆心为点
的外接圆的圆心为点 .
.
(1)求 与
与 轴的另一个交点D的坐标;
轴的另一个交点D的坐标;
(2)如果 恰好为
恰好为 的直径,且
的直径,且 的面积等于
的面积等于 ,求
,求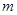 和
和 的值.
的值.
查看答案和解析>>
科目: 来源:2012-2013学年江苏省江都市甘棠中学七年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,已知:直线 交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
(1)求抛物线的解析式;
(2)若点D的坐标为(-1,0),在直线 上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
上有一点P,使ΔABO与ΔADP相似,求出点P的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使ΔADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013年江苏省南京市鼓楼区中考一模数学试卷(带解析) 题型:解答题
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨 元(
元( 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为 元.
元.
(1)求 与
与 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量 的取值范围;
的取值范围;
(2)若每个月的利润为2200元,求每件商品的售价应定为多少元?
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目: 来源:2013届江苏省扬州市蒋王中学九年级下学期第一次模拟数学试卷(带解析) 题型:解答题
如图,直线y= -x+3与x轴,y轴分别相交于点B、C,经过B、C两点的抛物线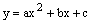 与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.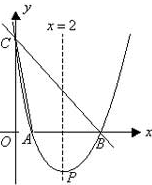
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连结AC.请问在x轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013年河南省平顶山市中考第二次调研测试(二模)数学试卷(带解析) 题型:解答题
如图,抛物线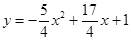 与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点产作PN⊥x轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并求出线段MN的最大值;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
查看答案和解析>>
科目: 来源:2012-2013学年浙江省湖州市长兴县实验初中九年级下学期期中调研数学试卷(带解析) 题型:解答题
如图,已知抛物线 (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(1)点B的坐标为 ,点C的坐标为 (用含b的代数式表示);
(2)若b=8,请你在抛物线上找点P,使得△PAC是直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你探索,在(1)的结论下,在第一象限内是否存在点Q,使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)如果存在,求出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012-2013学年浙江省湖州市长兴县实验初中八年级下学期期中调研数学试卷(带解析) 题型:解答题
某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(用含x的代数式表示)
(2)如果批发商希望通过销售这批T恤获利8750元,那么第二个月的单价应是多少元?
(3)要使批发商获利最多,那么第二个月的单价应是多少元,此时获得的最大利润是多少元?请说明理由,并写出必要的过程.
查看答案和解析>>
科目: 来源:2012-2013学年浙江省湖州十二中九年级第二学期期中考试数学试卷(带解析) 题型:解答题
某商人开始时,将进价为每件8元的某种商品按每件10元出售,每天可售出100件.他想采用提高售价的办法来增加利润,经试验,发现这种商品每件每提价l元,每天的销售量就会减少10件.
(1)写出售价x(元/件)与每天所得的利润y(元)之间的函数关系式;
(2)每件售价定为多少元,才能使一天的利润最大。
查看答案和解析>>
科目: 来源:2013届江苏省无锡市前洲中学九年级下学期期中考试数学试卷(带解析) 题型:解答题
阅读下列材料:
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+Bx+C=0的距离(d)计算公式是:d= .
.
例:求点P(1,2)到直线y= x-
x- 的距离d时,先将y=
的距离d时,先将y= x-
x- 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d= =
= .
.
解答下列问题:
如图2,已知直线y=- x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com