
科目: 来源:2013年江苏省兴化市安丰中学九年级一模数学试卷(带解析) 题型:解答题
如图,直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B坐标为(2, ),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
(1)求OH的长;
(2)若△OPQ的面积为S(平方单位).求S与t之间的函数关系式.并求t为何值时,△OPQ的面积最大,最大值是多少;
(3)设PQ与OB交于点M.①当△OPM为等腰三角形时,求(2)中S的值. ②探究线段OM长度的最大值是多少,直接写出结论.
查看答案和解析>>
科目: 来源:2013年江苏省兴化市安丰中学九年级一模数学试卷(带解析) 题型:解答题
某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行,并以各自的速度匀速行驶,途径配货站C,甲车先到达C地,并在C地用1小时配货,然后按原速度开往B地,乙车从B地直达A地,下图是甲、乙两车间的距离 (千米)与乙车出发
(千米)与乙车出发 (时)的函数的部分图像
(时)的函数的部分图像
(1)A、B两地的距离是 千米,甲车出发 小时到达C地;
(2)求乙车出发2小时后直至到达A地的过程中, 与
与 的函数关系式及
的函数关系式及 的取值范围,并在图中补全函数图像;
的取值范围,并在图中补全函数图像;
(3)乙车出发多长时间,两车相距150千米?
查看答案和解析>>
科目: 来源:2013届上海市虹口区中考二模数学试卷(带解析) 题型:解答题
已知:直线 交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线
交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线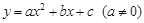 经过点A、B、C.
经过点A、B、C.
(1)求该抛物线的表达式;
(2)点D的坐标为(-3,0),点P为线段AB上一点,当锐角∠PDO的正切值为 时,求点P的坐标;
时,求点P的坐标;
(3)在(2)的条件下,该抛物线上的一点E在x轴下方,当△ADE的面积等于四边形APCE的面积时,求点E的坐标.
查看答案和解析>>
科目: 来源:2013届江苏省扬州市梅岭中学九年级第一次模拟考试数学试卷(带解析) 题型:解答题
抛物线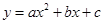 交
交 轴于
轴于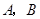 两点,交
两点,交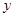 轴于点
轴于点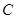 ,对称轴为直线
,对称轴为直线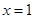 。且A、C两点的坐标分别为
。且A、C两点的坐标分别为 ,
,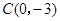 .
.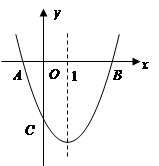
(1)求抛物线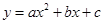 的解析式;
的解析式;
(2)在对称轴上是否存在一个点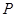 ,使
,使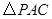 的周长最小.若存在,请求出点
的周长最小.若存在,请求出点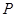 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013届湖北省天门市十一校九年级4月联考数学试卷(带解析) 题型:解答题
如图 ,在平面直角坐标系中,等腰直角
,在平面直角坐标系中,等腰直角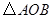 的斜边
的斜边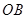 在
在 轴上,顶点
轴上,顶点 的坐标为
的坐标为 ,
, 为斜边上的高.抛物线
为斜边上的高.抛物线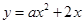 与直线
与直线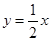 交于点
交于点 ,点
,点 的横坐标为
的横坐标为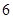 .点
.点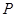 在
在 轴的正半轴上,过点
轴的正半轴上,过点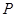 作
作 轴.交射线
轴.交射线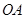 于点
于点 .设点
.设点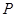 的横坐标为
的横坐标为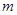 ,以
,以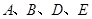 为顶点的四边形的面积为
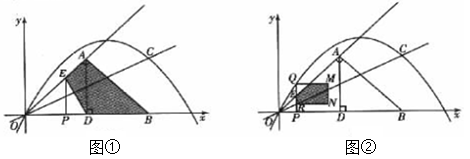
为顶点的四边形的面积为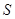 .
.
(1)求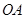 所在直线的解析式;
所在直线的解析式;
(2)求 的值;
的值;
(3)当 时,求
时,求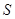 与
与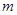 的函数关系式;
的函数关系式;
(4)如图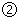 ,设直线
,设直线 交射线
交射线 于点
于点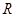 ,交抛物线于点
,交抛物线于点 .以
.以 为一边,在
为一边,在 的右侧作矩形
的右侧作矩形 ,其中
,其中 .直接写出矩形
.直接写出矩形 与
与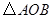 重叠部分为轴对称图形时
重叠部分为轴对称图形时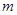 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2013届湖北省天门市十一校九年级4月联考数学试卷(带解析) 题型:解答题
某商店经营儿童益智玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件玩具售价不能高于40元. 设每件玩具的销售单价上涨了x元时(x为正整数),月销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件玩具的售价定为多少元时,月销售利润恰为2520元?
(3)每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
查看答案和解析>>
科目: 来源:2013届江西省景德镇市九年级下学期第二次质检数学试卷(带解析) 题型:解答题
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.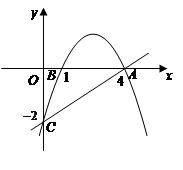
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.
查看答案和解析>>
科目: 来源:2013年江苏省南京市联合体(栖霞下关雨花台等)九年级中考一模数学试卷(带解析) 题型:解答题
(1)求二次函数y=x2-4x+1图象的顶点坐标,并指出当x在何范围内取值时,y随x的增大而减小;
(2)若二次函数y=x2-4x+c的图象与坐标轴有2个交点,求字母c应满足的条件.
查看答案和解析>>
科目: 来源:2013年江苏省南京市建邺区中考一模数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系 中,
中, 、
、 为
为 轴上两点,
轴上两点, 、
、 为
为 一上两点,经过点
一上两点,经过点 、
、 、
、 的抛物线的一部分
的抛物线的一部分 与经过点
与经过点 、
、
 的抛物线的一部分
的抛物线的一部分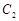 组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点
组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点 的坐标为
的坐标为 ,点
,点 是抛物线
是抛物线 的顶点.
的顶点.
(1)求 、
、 两点的坐标;
两点的坐标;
(2)“蛋线”在第四象限上是否存在一点 ,使得
,使得 的面积最大?若存在,求出
的面积最大?若存在,求出 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
(3)当 为直角三角形时,求
为直角三角形时,求 的值.
的值.
查看答案和解析>>
科目: 来源:2013年江苏省扬州市广陵区中考一模考试数学试卷(带解析) 题型:解答题
如图,已知直线 ,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线
,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线 上的一点,以点A、B、D为顶点作正方形.
上的一点,以点A、B、D为顶点作正方形.
(1)若图仅看作符合条件的一种情况,求出所有符合条件的点D的坐标;
(2)在图中,若点P以每秒1个单位长度的速度沿直线 从点O移动到点B,与此同时点Q以相同的速度从点A出发沿着折线A-B-C移动,当点P到达点B时两点停止运动.试探究:在移动过程中,△PAQ的面积最大值是多少?
从点O移动到点B,与此同时点Q以相同的速度从点A出发沿着折线A-B-C移动,当点P到达点B时两点停止运动.试探究:在移动过程中,△PAQ的面积最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com