
科目: 来源:2013届江苏省如皋市九年级中考模拟数学试卷(带解析) 题型:解答题
如图,抛物线与x轴相交于B,C两点,与y轴相交于点A,P(2a,-4a2+7a+2)(a是实数)在抛物线上,直线y=k x +b经过A,B两点.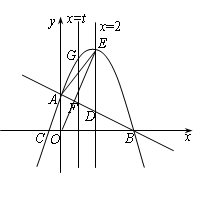
(1)求直线AB的解析式;
(2)平行于y轴的直线x=2交直线AB于点D,交抛物线于点E.
①直线x=t(0≤t≤4)与直线AB相交F,与抛物线相交于点G.若FG∶DE=3∶4,求t的值;
②将抛物线向上平移m(m>0)个单位,当EO平分∠AED时,求m的值.
查看答案和解析>>
科目: 来源:2013届江苏省南通市海安县九年级学业水平测试(一模)数学试卷(带解析) 题型:解答题
如图,抛物线y=-x2+mx+n与x轴分别交于点A(4,0),B(-2,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)M为第一象限内抛物线上一动点,点M在何处时,△ACM的面积最大;
(3)在抛物线的对称轴上是否存在这样的点P,使得△PAC为直角三角形?若存在,请求出所有可能点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013届江苏省南通市通州区九年级中考适应性考试(一模)数学试卷(带解析) 题型:解答题
已知:如图,直线 交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(1)求b的值;
(2)若点P是线段AB中垂线上的点,是否存在这样的点P,使△PBC成为直角三角形.若存在,试直接写出所有符合条件的点P的坐标;若不存在,试说明理由;
(3)点Q为线段AB上一个动点(点Q与点A、B不重合),QE∥AC,交BC于点E,以QE为边,在点B的异侧作正方形QEFG.设AQ=m,△ABC与正方形QEFG的重叠部分的面积为S,试求S与m之间的函数关系式,并写出m的取值范围.
查看答案和解析>>
科目: 来源:2013届江苏省南通市通州区九年级中考适应性考试(一模)数学试卷(带解析) 题型:解答题
某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.
| 时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
| 销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |

查看答案和解析>>
科目: 来源:2013届江苏省泰州市海陵区九年级中考二模数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中0A=2,0B=4,将△OAB绕点O顺时针旋转90°至△OCD,若已知抛物线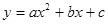 过点A、D、B.
过点A、D、B.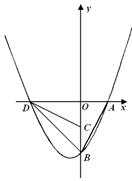

(1)求此抛物线的解析式;
(2)连结DB,将△COD沿射线DB平移,速度为每秒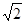 个单位.
个单位.
①经过多少秒O点平移后的O′点落在线段AB上?
②设DO的中点为M,在平移的过程中,点M、A、B能否构成等腰三角形?若能,求出构成等腰三角形时M点的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源:2013届江苏省泰州市海陵区九年级中考二模数学试卷(带解析) 题型:解答题
溱湖湿地风景区特色旅游项目:水上游艇. 旅游人员消费后风景区可盈利10元/人,每天消费人员为500人. 为增加盈利,准备提高票价,经调查发现,在其他条件不变的情况下,票价每涨1元,消费人员就减少 20人.
(1)现该项目要保证每天盈利6000元,同时又要旅游者得到实惠,那么票价应涨价多少元?
(2)若单纯从经济角度看,票价涨价多少元,能使该项目获利最多?
查看答案和解析>>
科目: 来源:2013届江苏省盐城市阜宁县东沟中学九年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,抛物线y=-x2+bx+c与x轴、y轴分别交于A(-1,0)、B(0,3)两点,顶点为D.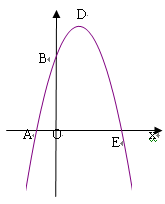
(1)求该抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积(3分)
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
查看答案和解析>>
科目: 来源:2013年江苏省南京市玄武区中考一模数学试卷(带解析) 题型:解答题
在函数中,我们规定:当自变量增加一个单位时,因变量的增加量称为函数的平均变化率.例如,对于函数y=3x+1,当自变量x增加1时,因变量y=3(x+1)+1=3x+4,较之前增加3,故函数y=3x+1的平均变化率为3.
(1)①列车已行驶的路程s(km)与行驶的时间t(h)的函数关系式是s=300t,该函数的平均变化率是 ;其蕴含的实际意义是 ;
②飞机着陆后滑行的距离y(m)与滑行的时间x(s)的函数关系式是y=-1.5x2+60x,求该函数的平均变化率;
(2)通过比较(1)中不同函数的平均变化率,你有什么发现;
(3)如图,二次函数y=ax2+bx+c的图像经过第一象限内的三点A、B、C,过点A、B、C作x轴的垂线,垂足分别为D、E、F,AM⊥BE,垂足为M,BN⊥CF,垂足为N,DE=EF,试探究△AMB与△BNC面积的大小关系,并说明理由.
查看答案和解析>>
科目: 来源:2013年重庆市育才成功学校中考一模数学试卷(带解析) 题型:解答题
已知: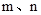 是方程
是方程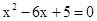 的两个实数根,且
的两个实数根,且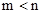 ,抛物线
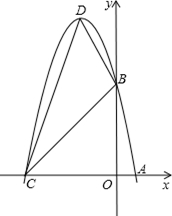
,抛物线 的图像经过点A(
的图像经过点A(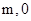 )、B(
)、B(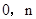 ).
).
(1)求这个抛物线的解析式;
(2) 设(1)中抛物线与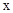 轴的另一交点为C,抛物线的顶点为D,
轴的另一交点为C,抛物线的顶点为D,
试求出点C、D的坐标和△BCD的面积;
(3) P是线段OC上的一点,过点P作PH⊥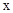 轴,与抛物线交于H点,
轴,与抛物线交于H点,
若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
查看答案和解析>>
科目: 来源:2013年四川省乐山市沙湾区九年级调研考试数学试卷(带解析) 题型:解答题
如图,二次函数 的图像过点
的图像过点 ,与
,与 轴交于点
轴交于点 .
.
(1)证明: (其中
(其中 是原点);
是原点);
(2)在抛物线的对称轴上求一点 ,使
,使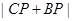 的值最小;
的值最小;
(3)若 是线段
是线段 上的一个动点(不与
上的一个动点(不与 、
、 重合),过
重合),过 作
作 轴的平行线,分别交此二次函数图像及
轴的平行线,分别交此二次函数图像及 轴于
轴于 、
、 两点 . 请问
两点 . 请问
是否存在这样的点 ,使
,使 . 若存在,
. 若存在,
请求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com