
科目: 来源:2013届浙江省绍兴县西藏民族中学九年级下第二次模拟考试数学卷(带解析) 题型:解答题
抛物线y=-x2+bx+c经过点A、B、C,已知A(-1,0),C(0,3).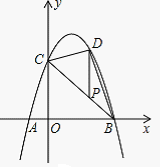
(1)求抛物线的解析式;
(2)求点B的坐标及直线BC的解析式;
(3)如图,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,求△BDC的面积的最大值。
查看答案和解析>>
科目: 来源:2013届上海市静安杨浦等六区初三一模(期末)数学试卷(带解析) 题型:解答题
如图,已知在△ABC中,∠A = 90°,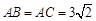 ,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.
,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.
(1)求PM的长;
(2)求y关于x的函数解析式,并写出它的定义域;
(3)联结MF、MG,当△PMF与△PMG相似时,求BM的长.
查看答案和解析>>
科目: 来源:2013届上海市静安杨浦等六区初三一模(期末)数学试卷(带解析) 题型:解答题
如图,在直角坐标系x O y中,二次函数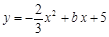 的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
(1)求这个二次函数的解析式;
(2)求∠BAC的正切值;
(3)如果点D在这个二次函数的图像上,且∠DAC = 45°,求点D的坐标.
查看答案和解析>>
科目: 来源:2013届上海市静安杨浦等六区初三一模(期末)数学试卷(带解析) 题型:解答题
已知:抛物线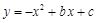 经过B(3,0)、C(0,3)两点,顶点为A.
经过B(3,0)、C(0,3)两点,顶点为A.
求:(1)抛物线的表达式;
(2)顶点A的坐标.
查看答案和解析>>
科目: 来源:2013届江苏省扬州市宝应县九年级中考网上阅卷适应性调研(一模)数学试卷(带解析) 题型:解答题
抛物线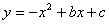 与x轴交与
与x轴交与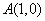 ,
,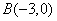 两点,
两点,
(1)求该抛物线的解析式;
(2)设(1)中的抛物线与y轴交于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013届浙江省湖州市九年级中考一模调研测试数学试卷(带解析) 题型:解答题
如图,平面直角坐标系xOy中, Rt△AOB的直角边OA在x轴的正半轴上,点B在第一象限,并且AB=3,OA=6,将△AOB绕点O逆时针旋转90度得到△COD.点P从点C出发(不含点C),沿射线DC方向运动,记过点D,P,B的抛物线的解析式为y=ax2+bx+c(a<0). 
(1)直接写出点D的坐标;
(2)在直线CD的上方是否存在一点Q,使得点D,O,P,Q四点构成的四边形是菱形,若存在,求出P与Q的坐标;
(3)当点P运动到∠DOP=45度时,求抛物线的对称轴;
(4)求代数式a+b+c的值的取值范围(直接写出答案即可).
查看答案和解析>>
科目: 来源:2013届浙江省湖州市九年级中考一模调研测试数学试卷(带解析) 题型:解答题
如图①是矩形包书纸的示意图,虚线是折痕,四个角均为大小相同的正方形,正方形的边长为折叠进去的宽度.
(1)现有一本书长为25cm,宽为20cm,厚度是2cm,如果按照如图①的包书方式,并且折叠进去的宽度是3cm,则需要书包纸的长和宽分别为多少?(请直接写出答案).
(2)已知数学课本长为26 cm,宽为18.5cm,厚为1cm,小明用一张面积为1260cm2的矩形书包纸按如图①包好了这本书,求折进去的宽度.
(3)如图②,矩形ABCD是一张一个角(△AEF)被污损的书包纸,已知AB=30,BC=50,AE=12,AF=16,要使用没有污损的部分包一本长为19,宽为16,厚为6的字典,小红认为只要按如图②的剪裁方式剪出一张面积最大的矩形PGCH就能包好这本字典. 设PM=x,矩形PGCH的面积为y,当x取何值时y最大?并由此判断小红的想法是否可行.
查看答案和解析>>
科目: 来源:2013年广东省广州市南沙区中考一模数学试卷(带解析) 题型:解答题
如图1,已知抛物线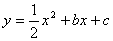 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.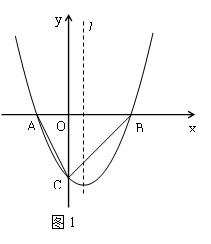
(1)求该抛物线的函数表达式;
(2)设P是(1)中抛物线上的一个动点,以P为圆心,R为半径作⊙P,求当⊙P与抛物线的对称轴l及x轴均相切时点P的坐标.
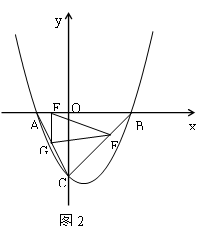
(3)动点E从点A出发,以每秒1个单位长度的速度向终点B运动,动点F从点B出发,以每秒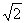 个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的
个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的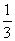 ?
?
查看答案和解析>>
科目: 来源:2013届湖北省襄阳市襄城区中考适应性考试数学试卷(带解析) 题型:解答题
矩形OABC在平 面直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=- x与BC边相交于D点.
x与BC边相交于D点.
(1)若抛物线y=ax- x经过点A,试确定此抛物线的解析式;
x经过点A,试确定此抛物线的解析式;
(2)在(1)中的抛物线的对称轴上取一点E,求出EA+ED的最小值;
(3)设(1)中的抛物线的对称轴与直线OD交于点M,点P为对称轴上一动点,以P、O、M为顶点的三角形与△OCD相似,求符合条件的点P的坐标.
查看答案和解析>>
科目: 来源:2013届广西大学附属中学九年级11月月考数学试卷(带解析) 题型:解答题
如图,某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.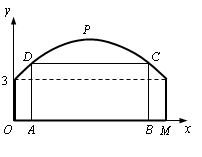
(1) 直接写出点M及抛物线顶点P的坐标;
(2) 求出这条抛物线的函数解析式;
(3) 若要搭建一个矩形“支撑架”AD- DC- CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com