
科目: 来源:2010届江西省新余九中初二年级上学期期中考试数学试卷 题型:单选题
如图1,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使
△ABC≌△DEF,不能添加的一组条件是 ( )
| A.∠B=∠E,BC=EF | B.BC=EF,AC=DF |
| C.∠A=∠D,∠B=∠E | D.∠A=∠D,BC=EF |
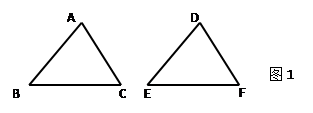
查看答案和解析>>
科目: 来源:2011届重庆市西南师大附中初二上学期数学期中试卷 题型:单选题
如图,在△ABC中,DE∥BC交AB、AC于点D、E,AD=1,BD=2,那么,△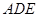 与△
与△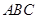 面积的比为( )
面积的比为( )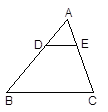
A. 1∶2 B. 1∶3 C. 1∶4 D. 1∶9
查看答案和解析>>
科目: 来源:2010年吉林省长春外国语学校初三上学期第一次月考数学卷 题型:单选题
已知直角三角形中30°角所对的直角边为2㎝,则斜边的长为( )。
| A. 2 ㎝ | B. 4 ㎝ | C. 6 ㎝ | D. 8㎝ |
查看答案和解析>>
科目: 来源:2010年吉林省长春外国语学校初三上学期第一次月考数学卷 题型:单选题
下列几种说法:①全等三角形的对应边相等;②面积相等的两个三角形全等;
③周长相等的两个三角形全等;④全等的两个三角形一定重合。其中正确的是( )。
| A.①② | B.②③ | C.③④ | D.①④ |
查看答案和解析>>
科目: 来源:2013年初中毕业升学考试(贵州六盘水卷)数学(带解析) 题型:解答题
(1)观察发现
如图(1):若点A、B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:
作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
如图(2):在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:
作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 .
(2)实践运用
如图(3):已知⊙O的直径CD为2,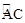 的度数为60°,点B是
的度数为60°,点B是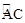 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为 .
的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为 .
(3)拓展延伸
如图(4):点P是四边形ABCD内一点,分别在边AB、BC上作出点M,点N,使PM+PN的值最小,保留作图痕迹,不写作法.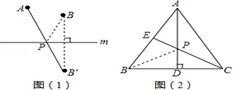

查看答案和解析>>
科目: 来源:2012-2013学年山西农业大学附属中学七年级下学期期末考试数学试卷(带解析) 题型:解答题
如图,两条公路相交,在A、B两处是两个居民区,邮政局要在居民区旁边修建一个邮筒,为了使邮寄和取送方便,要使邮筒到两条路的距离相等,并且到两个居民区的距离也相等,请你找到一个这样的点。
查看答案和解析>>
科目: 来源:2012-2013学年河南省郑州市第二学期期末考试七年级数学试卷(带解析) 题型:解答题
如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?(请把思考过程补充完整)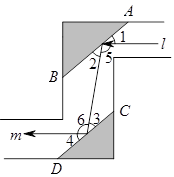
理由:
因为:AB∥CD(已知),
所以:∠2=∠3( ).
因为:∠1=∠2,∠3=∠4(已知).
所以:∠1=∠2=∠3=∠4(等量代换).
所以:180°-∠1-∠2=180°-∠3-∠4(平角定义).
即:___________(等量代换).
所以:__________( ).
查看答案和解析>>
科目: 来源:2013届安徽省毫州市风华中学九年级上学期期末测试数学试卷(二)(带解析) 题型:解答题
如图,在△ABC中,∠CAB=120°,AD是∠CAB的平分线,AC=6,AB=10.
(1)求 ;
;
(2)求AD的长.
查看答案和解析>>
科目: 来源:2013年初中毕业升学考试(辽宁鞍山卷)数学(带解析) 题型:解答题
如图,已知线段a及∠O,只用直尺和圆规,求做△ABC,使BC=a,∠B=∠O,∠C=2∠B(在指定作图区域作图,保留作图痕迹,不写作法)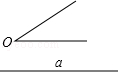
查看答案和解析>>
科目: 来源:2013年初中毕业升学考试(浙江绍兴卷)数学(带解析) 题型:解答题
如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm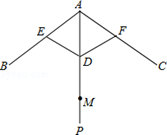
| 伞架 | DE | DF | AE | AF | AB | AC |
| 长度 | 36 | 36 | 36 | 36 | 86 | 86 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com