
科目: 来源:2011年河北省唐山市玉田县第三中学八年级上学期期中考试数学卷 题型:解答题
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
【小题1】请找出图2中的全等三角形,_____≌____并给予证明(说明:结论中不得含有未标识的字母);
【小题2】证明:DC⊥BE.
查看答案和解析>>
科目: 来源:2011年河北省唐山市玉田县八年级第一学期期中考试数学卷 题型:解答题
『问题情境』勾股定理是一条古老的数学定理,它有多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行了证明.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其它星球“人”进行第一次“谈话”的语言.
『定理表述』请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述).
『尝试证明』以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理.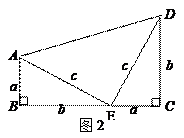
『知识拓展』利用图2中的直角梯形,我们可以证明<.其证明步骤如下:
∵BC=a+b,AD= ,
又在直角梯形ABCD中,BC AD(填大小关系),
即 .
∴<.
查看答案和解析>>
科目: 来源:2011年河北省唐山市玉田县八年级第一学期期中考试数学卷 题型:解答题
【小题1】观察与发现:
在一次数学课堂上,老师把三角形纸片ABC(AB>AC)沿过A点的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).有同学说此时的△AEF是等腰三角形,你同意吗?请说明理由.
【小题2】实践与运用
将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点 处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠
处,折痕为EG(如图④);再展平纸片(如图⑤).试问:图⑤中∠ 的大小是多少?(直接回答,不用说明理由).
的大小是多少?(直接回答,不用说明理由).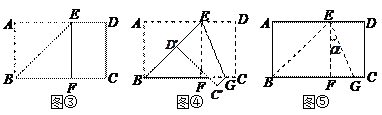
查看答案和解析>>
科目: 来源:2010年江西省新余九中八年级上学期期中考试数学卷 题型:解答题
如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在AE的
异侧,BD⊥AE于D,CE⊥AE于E,
【小题1】求证:BD=DE+CE;
【小题2】若直线AE绕A点旋转到图2位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何,请证明;
【小题3】若直线AE绕A点旋转到图3时(BD>CE)其余条件不变,BD与DE、CE的关系怎样?请直接写出结果,不需证明
查看答案和解析>>
科目: 来源:2010年江西省新余九中八年级上学期期中考试数学卷 题型:解答题
如图,公园有一条“ ”字形道路
”字形道路 ,其中
,其中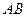 ∥
∥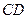 ,在
,在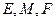 处各有一个小石凳,且
处各有一个小石凳,且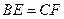 ,
,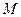 为
为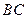 的中点,请问三个小石凳是否在一条直线上?说出你推断的理由.
的中点,请问三个小石凳是否在一条直线上?说出你推断的理由.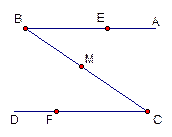
查看答案和解析>>
科目: 来源:2011-2012年江苏省南通市幸福中学八年级上学期期中考试数学卷 题型:解答题
(本题12分)数学课上,李老师出示了如下框中的题目.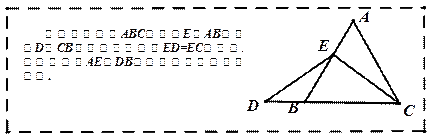
小敏与同桌小聪讨论后,进行了如下解答:
【小题1】(1)特殊情况,探索结论
当点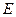 为
为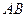 的中点时,如图1,确定线段
的中点时,如图1,确定线段 与
与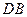 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:
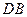 (填“>”,“<”或“=”).
(填“>”,“<”或“=”). 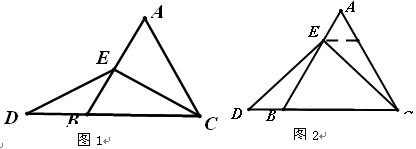
|
|
 与
与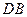 的大小关系是:
的大小关系是:
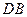 (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点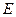 作
作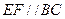 ,交
,交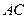 于点
于点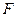 .
.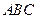 中,点
中,点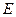 在直线
在直线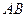 上,点
上,点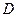 在直线
在直线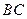 上,且
上,且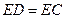 .若
.若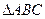 的边长为1,
的边长为1,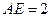 ,求
,求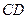 的长(请你直接写出结果).
的长(请你直接写出结果). 查看答案和解析>>
科目: 来源:2011-2012年江苏省南通市幸福中学八年级上学期期中考试数学卷 题型:解答题
(本题10分).如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
【小题1】(1)求证:DE平分∠BDC;
【小题2】(2)若点M在DE上,且DC=DM,求证:ME=BD.
查看答案和解析>>
科目: 来源:2011-2012年江苏省南通市通州区十总中学八年级上学期期中考试数学卷 题型:解答题
(本题满分8分)
在 中,
中, ,点
,点 是直线
是直线 上一点(不与
上一点(不与 重合),以
重合),以 为一边在
为一边在 的右侧作
的右侧作 ,使
,使 ,连接
,连接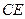 .
.
【小题1】(1)如图1,当点 在线段
在线段 上,如果
上,如果 ,则
,则 度;
度;
【小题2】(2)设 ,
, .
.
①如图2,当点 在线段
在线段 上移动,则
上移动,则 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点 在直线
在直线 上移动,则
上移动,则 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.
查看答案和解析>>
科目: 来源:2011-2012年江苏省南通市通州区十总中学八年级上学期期中考试数学卷 题型:解答题
(本题满分6分)
如图所示,点P是等边△ABC外一点,∠APC =60°, PA、BC交于点D,
求证:
查看答案和解析>>
科目: 来源:2011-2012年江苏省南通市通州区十总中学八年级上学期期中考试数学卷 题型:解答题
(本题满分6分)
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28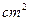 ,AB=20cm,AC=8cm,求DE的长.
,AB=20cm,AC=8cm,求DE的长.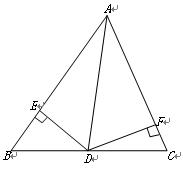
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com