
科目: 来源:2011-2012年重庆市开县西街初级中学九年级模拟考试数学卷二 题型:解答题
(本小题满分6分)尺规作图:已知线段a,作一个等腰 ,使底边长为a,底边上的高为
,使底边长为a,底边上的高为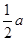 .(要求:写出已知求作,保留作图痕迹,在所作图中标出必要的字母,不写作法和结论)
.(要求:写出已知求作,保留作图痕迹,在所作图中标出必要的字母,不写作法和结论)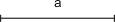
已知:
求作:
查看答案和解析>>
科目: 来源:2012年人教新课标版中考综合模拟数学卷(16) 题型:解答题
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.
【小题1】如图1,在等腰三角形ABC中,AB=AC,AC边上的高为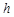 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为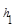 、
、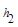 .连接AM,可得结论
.连接AM,可得结论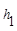 +
+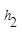 =
=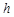 .当点M在BC延长线上时,
.当点M在BC延长线上时,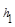 、
、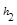 、
、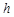 之间的等量关系式是 .(直接写出结论不必证明).
之间的等量关系式是 .(直接写出结论不必证明).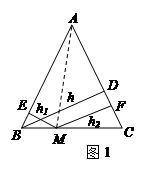
【小题2】应用:平面直角坐标系中有两条直线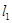 :
: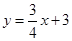 、
、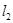 :
: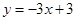 ,若
,若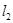 上的一点M到
上的一点M到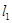 的距离是1.请运用(1)的条件和结论求出点M的坐标.
的距离是1.请运用(1)的条件和结论求出点M的坐标.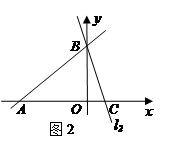
查看答案和解析>>
科目: 来源:2012年人教新课标版中考综合模拟数学卷(16) 题型:解答题
图(a)、图(b)是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)中,分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.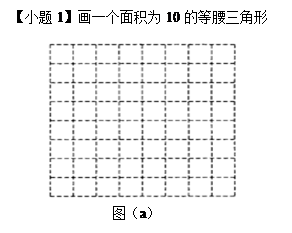
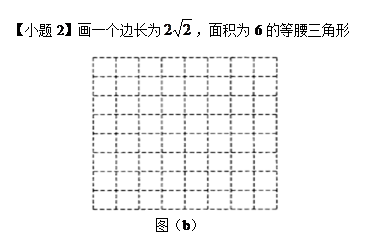
查看答案和解析>>
科目: 来源:2011-2012学年广西省贵港市木格中学中考模拟试题数学试卷(一) 题型:解答题
如图,点B、D、C、F在一条直线上,且BD = FC,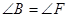 ,AB = EF。求证△ABC≌△EFD.
,AB = EF。求证△ABC≌△EFD.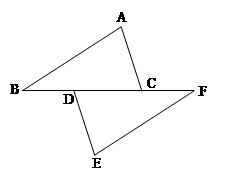
查看答案和解析>>
科目: 来源:2012年人教新课标版中考综合模拟数学卷(4) 题型:解答题
如图10-1-2(1),10-1-2(2),四边形ABCD是正方形,M是AB延长线上一点。直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F。
【小题1】如图10-1-2(1),当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是 ;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ;
③请证明你的上述两猜想。
【小题2】如图10-1-2(2),当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系。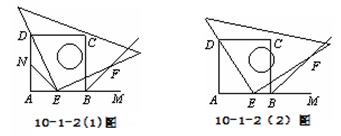
查看答案和解析>>
科目: 来源:2011年江苏省洋思中学九年级月考数学卷 题型:解答题
( 本题满分12分)
【小题1】(1)动手操作:
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。
【小题2】(2)观察发现小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由
(3)实践与运用:
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小。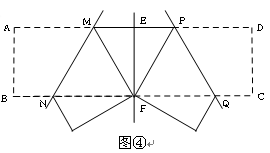
查看答案和解析>>
科目: 来源:2011-2012年福建省永定县仙师中学八年级第一学期第一次月考数学卷 题型:解答题
(10分)在△ABC中,BE、CF分别是AC、AB两条边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。求证:AG=AD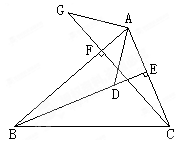
查看答案和解析>>
科目: 来源:2011-2012年福建省永定县仙师中学八年级第一学期第一次月考数学卷 题型:解答题
(10分)如图,点D,E分别在AC,AB上.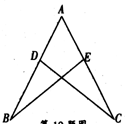
【小题1】(1) 已知,BD=CE,CD=BE,求证:AB=AC;
【小题2】(2) 分别将“BD=CE”记为①,“CD=BE” 记为②,“AB=AC”记为③.添加条件①、③,以②为结论构成命题1,添加条件②、③以①为结论构成命题2.命题1是命题2的 命题,命题2是
命题.(选择“真”或“假”填入空格).
查看答案和解析>>
科目: 来源:2011-2012年福建省永定县仙师中学八年级第一学期第一次月考数学卷 题型:解答题
(10分)如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
求证:BC∥EF.
查看答案和解析>>
科目: 来源:2011-2012年福建省永定县仙师中学八年级第一学期第一次月考数学卷 题型:解答题
(9分)已知:如图,四边形ABCD中,AB∥CD ,AD∥BC。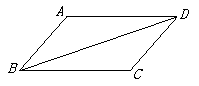
求证:△ABD≌△CDB。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com