
科目: 来源:2010-2011学年安徽省安庆市八年级第二学期质量检测数学卷 题型:解答题
如图是用硬纸板做成的四个全等的直角三角形(两直角边长分别是a,b,斜边长为c)和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形,并利用此图形证明勾股定理.
查看答案和解析>>
科目: 来源:2011-2012学年湖北省宜昌市长阳县九年级第一学期期末模拟数学卷 题型:解答题
如图,在△ABC中,AB=AC.
【小题1】(1)请作出AB的中垂线DE,交AC于D交AB于E.(不写作法,保留作图痕迹)
【小题2】(2)如果BD=BC,求∠A的度数.(8分)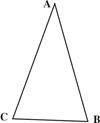
查看答案和解析>>
科目: 来源:2011-2012学年湖北省宜昌市长阳县八年级第一学期期末模拟数学卷 题型:解答题
如右图,5米长的一根木棒AB靠在墙上A点处,落地点为B,已知OB=4米.现设计从O点处拉出一根铁丝来加固该木棒.
【小题1】(1)请你在图中画出铁丝最短时的情形.
【小题2】(2)如果落地点B向墙角O处移近2米,则木棒上端A上移是少于2米,还是多于2米?说明理由.
【小题3】(3)如果从O点处拉出一根铁丝至AB的中点P处来加固木棒,这时铁丝在木棒移动后,需要加长还是剪短?还是不变?请说明理由.(8分)
查看答案和解析>>
科目: 来源:2011-2012学年河南省长葛市创新中学八年级上学期期末模拟考试数学卷 题型:解答题
如图,在直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.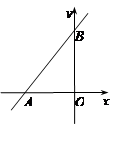
【小题1】(1)求k的值;
【小题2】(2)若P为直线AB上一动点,P点运动到什么位置时,△PAO是以OA为底的等腰三角形,求点P的坐标;
【小题3】(3)在(2)的条件下,连结PO,△PBO是等腰三角形吗?如果是,试说明理由,如果不是,请在线段AB上求一点C,使得△CBO是等腰三角形.
查看答案和解析>>
科目: 来源:2011-2012学年浙江省平阳县昆阳镇第三中学九年级第二次月考数学卷 题型:解答题
(本小题14分)如图,已知在△ABC中,∠B=90°,AB=6cm,BC=8cm,点 P
P 从点A开始,沿AB边向点B以1cm/S的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,(其中一点到达终点,另一点也停止运动),设经过t秒?
从点A开始,沿AB边向点B以1cm/S的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,(其中一点到达终点,另一点也停止运动),设经过t秒?
【小题1】(1)(4分)如果P、Q分别从A、B两点同时出发,那么几秒后,△PBQ的面积等于△ABC的面积的 ?
?
【小题2】(2)(5分)若P、Q分别从A、B两点出发,那么几秒后,PQ的长度等于6cm?
【小题3】(3)(5分)P、Q在移动的过程中,是否存在某一时刻t,使得PQ∥AC,若存在求出t的值,若不存在请说明理由?
查看答案和解析>>
科目: 来源:2011-2012学年浙江省杭州市萧山瓜沥片八年级12月月考数学卷 题型:解答题
如图,在△ABC中,已知AB=AC,∠BAC=90o,BC=6cm,,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒2厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度运动,连结AD、AE,设运动时间为t秒.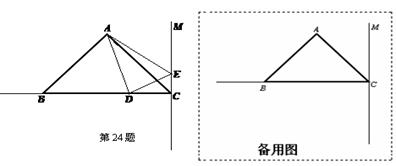
【小题1】(1)求AB的长;
【小题2】(2)当t为多少时,△ABD的面积为6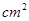 ?
?
【小题3】(3)当t为多少时,△ABD≌△ACE,并简要说明理由(可在备用图中画出具体图形).
查看答案和解析>>
科目: 来源:2011-2012学年浙江省杭州市萧山瓜沥片八年级12月月考数学卷 题型:解答题
已知:如图,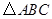 中,
中,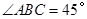 ,
, 于
于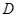 ,
,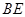 平分
平分 ,且
,且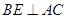 于
于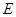 ,与
,与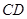 相交于点
相交于点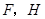 是
是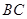 边的中点,连结
边的中点,连结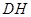 与
与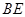 相交于点
相交于点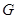 .
.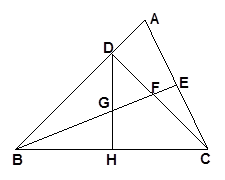
【小题1】(1)说明: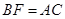 ;
;
【小题2】(2)说明: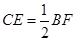 ;
;
【小题3】(3)试探索 ,
,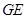 ,
, 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源:2011-2012学年浙江省杭州市萧山瓜沥片八年级12月月考数学卷 题型:解答题
问题背景:在△ABC中,AB、BC、AC三边的长分别为、、, 求这个三角形的面积.
求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面 积.
积.
【小题1】(1)请你将△ABC的面积直接填写在横线上.____ ▲__ _____
_____
【小题2】(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为a、2a、a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
【小题3】(3)若△ABC三边的长分别为、、2(m>0,n>0,且m≠n),试运用构图法求出这三角形的面积.
查看答案和解析>>
科目: 来源:2011-2012学年浙江省杭州市萧山临浦片八年级12月月考数学卷 题型:解答题
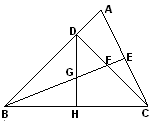
(本题10分)如图,已知在等腰直角三角形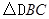 中,
中,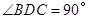 ,
, 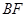 平分
平分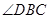 ,与
,与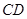 相交于点
相交于点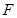 ,延长
,延长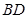 到
到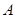 ,使
,使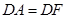 ,
,
【小题1】(1)试说明: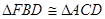 ;
;
【小题2】(2)延长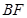 交
交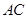 于
于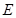 ,且
,且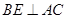 ,)试说明:
,)试说明: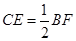 ;
;
【小题3】(3)在⑵的条件下,若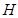 是
是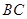 边的中点,连结
边的中点,连结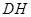 与
与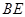 相交于点
相交于点 .
.
试探索 ,
, ,
, 之间的数量关系,并说明理由
之间的数量关系,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com