
科目: 来源:2011-2012学年福建省泉州市德化县七年级下学期质量监控数学卷(带解析) 题型:解答题
已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题: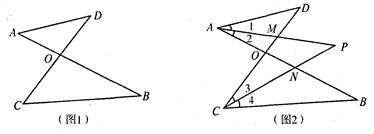
(1)在图1中,若∠A+∠D=80°,则∠B+∠C= ;仔细观察,在图2中“8字形”的个数: 个;
(2)在图2中,若∠DAO=50°,∠OCB=40°,∠P=35°,试求∠D的度数;
(3)在图2中,若设∠D=x°,∠B=y°,其它条件不变,试求∠P的度数.
查看答案和解析>>
科目: 来源:2011-2012学年福建省泉州市德化县七年级下学期质量监控数学卷(带解析) 题型:解答题
如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D、E,∠AFD=158°.求: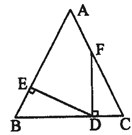
(1)∠C的度数;
(2)∠EDF的度数。
查看答案和解析>>
科目: 来源:2011-2012学年福建省泉州市德化县七年级下学期质量监控数学卷(带解析) 题型:解答题
已知一个多边形的每个内角都比相邻外角的3倍还多20°,求这个多边形的内角和。
查看答案和解析>>
科目: 来源:2012届江苏省无锡市华仕初中中考模拟(5)数学卷(带解析) 题型:解答题
学校选修课上木工制作小组决定制作等腰三角形积木,现从某家具厂找来如图所示的梯形边角余料(单位:cm).且制作方案如下:
(1)三角形中至少有一边长为10 cm;
(2)三角形中至少有一边上的高为8 cm请你画出三种不同的分割线,并求出相应图形面积.(要求画出的三个等腰三角形的面积不等)
查看答案和解析>>
科目: 来源:2012届江苏响水初三第二次模拟数学试卷(带解析) 题型:解答题
已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD。
【小题1】如图1,以AB为边在△ABC外作等腰△ABE,其中AB=AE,,试证明BD=CE;
【小题2】如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4,求BD的长;
【小题3】如图3,若∠ACB为锐角,作AH⊥BC于H,当BD2=4AH2+BC2时,问∠DAC与∠ABC有怎样的关系,直接写出结论(不需要证明)。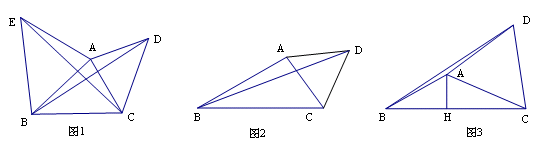
查看答案和解析>>
科目: 来源:2012届福建永安九年级学业质量检测考试数学试卷(带解析) 题型:解答题
阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似地,可以在等腰三角形中,建立边角之间的联系。我们定义:等腰三角形中底边长与腰长的比叫做顶角正对(sad)。如图1,在⊿ABC中,AB=AC,顶角A的正对记作sadA,这时sadA= 。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
【小题1】计算:sad60°= ▲
【小题2】对于0°<A<90°,∠A的正对值sadA的取值范围是 ▲ ;
【小题3】如图2,已知△DEF中,∠E=90°,cosD= ,试求sadD的值。
,试求sadD的值。
查看答案和解析>>
科目: 来源:2012届河南安阳九年级5月中考模拟考试数学试卷(带解析) 题型:解答题
已知,如图,在△ABC中AB=AC,点P是△ABC的中线AD上的任意一点(不与点A重合.将线段AP绕点A逆时针旋转到AQ,使.∠PAQ=∠BAC,连接BP,CQ.
【小题1】求证:BP=CQ
【小题2】设直线BP与直线CQ相交于点E,∠BAC=α,∠BEC="β," ①若点P在线段AD上移动(不与点A重合),则“α与β之间有怎样的数量关系?并说明理由. ②若点P在直线AD上移动(不与点A重合).则α与β之间有怎样的数量关系?请直接写出你的结论.
查看答案和解析>>
科目: 来源:2012届福建尤溪初中毕业学业质量检测数学试卷(带解析) 题型:解答题
两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等?为什么?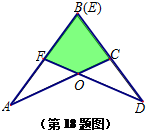
查看答案和解析>>
科目: 来源:2012届福建厦门外国语学校九年级中考模拟数学试卷(带解析) 题型:解答题
已知等腰△ABC中,AB=AC,D是BC的中点,将三角板中的90°角的顶点绕D点在△ABC内旋转,角的两边分别与AB、AC交于E、F,且点E、F不与A、B、C三点重合.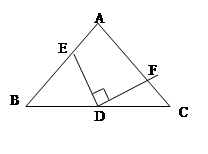
【小题1】如果∠A=90°求证:DE=DF
【小题2】如果DF//AB,则结论:“四边形AEDF为直角梯形”是否正确,若正确,请证明;若不正确,请画出草图举反例
查看答案和解析>>
科目: 来源:2012届辽宁省丹东七中九年级下学期第二次模拟考试数学卷(带解析) 题型:解答题
在Rt△ABC中,∠ACB=90°,tan∠BAC= . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
【小题1】若过点D作DE⊥AB于E,连结CF、EF、CE,如图1. 设 ,
,
则k = ;
【小题2】若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示. 求证:BE-DE=2CF;
【小题3】若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com