
科目: 来源:2012届广西武鸣中考第一次模拟数学试卷(带解析) 题型:解答题
如图9所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
(1)分别写出点A、B两点的坐标;
(2)作出△ABC关于坐标原点成中心对称的△A1B1C1;
(3)作出点C关于是x轴的对称点P. 若点P向右平移x个单位长度后落在△A1B1C1的内部,请直接写出x的取值范围.
查看答案和解析>>
科目: 来源:2011-2012学年重庆开县南雅初级中学八年级期末数学试卷(带解析) 题型:解答题
如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90o,且EF交正方形外角的平分线CF于点F.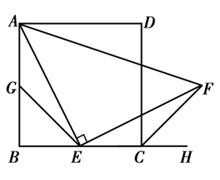
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.
查看答案和解析>>
科目: 来源:2011-2012学年江西九江七年级第二学期期中联考数学试卷(带解析) 题型:解答题
如图,已知在△ 中,∠A=∠B
中,∠A=∠B 
(1)请你添加一个与直线AB有关的条件,由此可推得CE是∠ACD的角平分线(只添加条件,不说理由);
(2)请你添加一个与∠A有关的条件,由此可推得CE是∠ACD的角平分线. (要写出理由)
查看答案和解析>>
科目: 来源:2011-2012学年福建福州连江兴海学校八年级下期中考数学试卷(带解析) 题型:解答题
定义:三边长和面积都是整数的三角形称为“整数三角形”.数学兴趣小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
⑴ 小亮用12根火柴棒,摆成(如右)示意图所示的“整数三角形”;
⑵ 小颖用小亮的方法分别用24根和30根火柴棒摆出直角“整数三角形”;
⑶ 小辉是一个爱动脑筋,喜欢创新的学生,他受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
请你画出小颖和小辉摆出的“整数三角形”的示意图.
(友情提示:在所画的示意图中每边须标出所需火柴棒根数.)
查看答案和解析>>
科目: 来源:2011-2012学年安徽全椒八年级下期末数学试卷(沪科版)(带解析) 题型:解答题
温州市处于东南沿海,夏季经常遭受台风袭击,一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处,以每小时10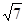 千米的速度向东偏南30°的BC方向移动,距台风中心200千米的范围是受台风严重影响的区域。试问:
千米的速度向东偏南30°的BC方向移动,距台风中心200千米的范围是受台风严重影响的区域。试问:
(1)台风中心在移动过程中离温州市最近距离是多少千米?
(2)温州市A是否受台风影响?若不会受到,请说明理由;由,若会受到,求出温州市受台风严重影响的时间.
查看答案和解析>>
科目: 来源:2011-2012学年江苏兴化板桥初级中学八年级下学期期末考试数学卷(带解析) 题型:解答题
如图,凸四边形ABCD中,点E在边CD上,连接AE、BE.给出下列五个关系式:①AD∥BC; ②DE=EC; ③∠1=∠2; ④∠3=∠4; ⑤AD+BC="AB" .将其中的三个关系式作为已知条件、另外两个关系式作为结论,可以构成一些命题(下面各小题的命题须符合此要求).
(1)共计能够成 个命题;
(2)写出三个真命题:
①如果 、 、 ,那么 、 ;
②如果 、 、 ,那么 、 ;
③如果 、 、 ,那么 、 .
请选择上述三个命题中的一个写出它是真命题的理由:
证明:我选择证明命题 (填序号),理由如下:
(第28题图)
(3)请写出一个假命题(不必说明理由):
如果 、 、 ,那么 、 .
查看答案和解析>>
科目: 来源:2011-2012学年江苏省太仓市七年级期中考试数学卷(带解析) 题型:解答题
探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?已知:如图,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:_______________________________.
查看答案和解析>>
科目: 来源:2011-2012学年江苏省太仓市七年级期中考试数学卷(带解析) 题型:解答题
如图,已知△ABC中,AD是高,AE是角平分线.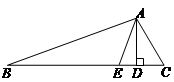
(1)若∠B=20°,∠C=60°,则∠EAD=_______°;
(2)若∠B=a°,∠C=b°(b>a),试通过计算,用a、b的代数式表示∠EAD的度数;
(3)特别地,当△ABC为等腰三角形(即∠B=∠C)时,请用一句话概括此时AD和AE的位置关系:______________________________.
查看答案和解析>>
科目: 来源:2012届湖南衡阳市初中学业水平模拟考试数学卷(带解析) 题型:解答题
在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.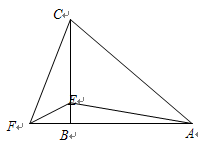
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30º,求∠ACF度数.
查看答案和解析>>
科目: 来源:2012届浙江省四校九年级联考数学卷(带解析) 题型:解答题
阅读材料:如图1:直线 ,点A,B,C,D分别在
,点A,B,C,D分别在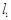 和
和 上,因为“两平行线间的距离处处相等”,所以
上,因为“两平行线间的距离处处相等”,所以 ,
, .
.
解决问题:如图2:在梯形ABCD中,AB∥CD,AC,BD相交于点O,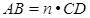 (n>1的正实数),梯形ABCD的面积为S.请回答下列问题:
(n>1的正实数),梯形ABCD的面积为S.请回答下列问题:
(1)请直接写出相应的值:①当n=2时,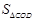 = ▲ S;②当n=3时,
= ▲ S;②当n=3时,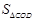 = ▲ S;
= ▲ S;
③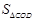 = ▲ S(用n的代数式表示);
= ▲ S(用n的代数式表示);
(2)如图3,点E,F分别在AD,BC的中点, EF分别交AC,BD于M,N,,求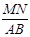 的值(用n的代数式表示);
的值(用n的代数式表示);
(3)在(2)中,根据上面的结论,当 时,直接写出n的值.
时,直接写出n的值.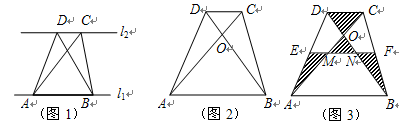
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com