
科目: 来源:2012年初中毕业升学考试(广东珠海卷)数学(带解析) 题型:解答题
如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.
(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状.(只写结果)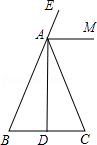
查看答案和解析>>
科目: 来源:2011-2012学年浙江杭州采荷中学七年级下期3月月考数学试卷(带解析) 题型:解答题
如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=500,∠C=600,求∠DAE和∠BOA的度数。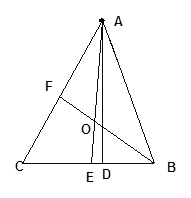
查看答案和解析>>
科目: 来源:2011-2012学年浙江杭州采荷中学七年级下期3月月考数学试卷(带解析) 题型:解答题
如图,已知∠A=∠D,AB="DE,AF=DC" ,请问图中有哪几对全等三角形?并任选其中一对给予证明。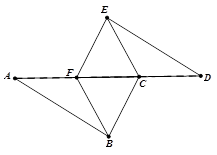
查看答案和解析>>
科目: 来源:2011-2012学年浙江杭州采荷中学七年级下期3月月考数学试卷(带解析) 题型:解答题
如图,△ABC中,∠B=50°,AD平分∠BAC, ∠ADC=80°,求∠C的度数。
查看答案和解析>>
科目: 来源:2011-2012学年浙江嘉兴九校七年级下学期期中考试数学试卷(带解析) 题型:解答题
一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ恰好分别经过点B、C.△ABC中,∠A=50°.
(1)如图1,则∠ABC+∠ACB= 度,∠XBC+∠XCB= 度;
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.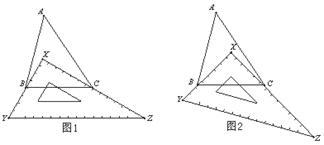
查看答案和解析>>
科目: 来源:2011-2012学年浙江嘉兴九校七年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE。试说明下列结论正确的理由:(1) ∠C=∠E; (2) AB=AD.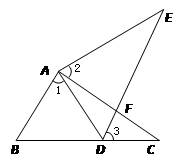
查看答案和解析>>
科目: 来源:2011-2012学年江苏泰兴济川中学八年级上期期末考试数学试卷(带解析) 题型:解答题
已知,如图:在△ABC中,∠ABC = 70°,∠ACB = 50°,E分别为AC、AB上的点,且BE = CD,G、M、N分别为BC、BD、CE的中点。
(1) 求∠MGN与∠A的度数相等吗?说明理由。
(2) 判断△GMN的形状,说明理由。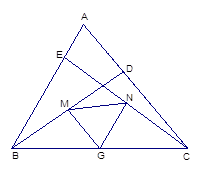
查看答案和解析>>
科目: 来源:2011-2012学年江苏泰兴济川中学八年级上期期末考试数学试卷(带解析) 题型:解答题
如图,△ABC中,AB = AC,中线BD、CE相交于O,线段OB、OC相等吗?请说明理由。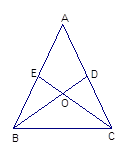
查看答案和解析>>
科目: 来源:2012届浙江省丽水市中考模拟试卷5数学试卷(带解析) 题型:解答题
已知:△ABC中,AB=10;
⑴如图①,若点D、E分别是AC、BC边的中点,求DE的长;
⑵如图②,若点A1、A2把AC边三等分,过A1、A2作AB边的平行线,分别交BC边于点B1、B2,求A1B1+A2B2的值;
⑶如图③,若点A1、A2、…、A10把AC边十一等分,过各点作AB边的平行线,分别交BC边于点B1、B2、…、B10。根据你所发现的规律,直接写出A1B1+A2B2+…+A10B10的结果.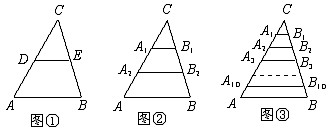
查看答案和解析>>
科目: 来源:2012届江苏省淮安市清浦区清浦中学中考模拟试卷2数学试卷(带解析) 题型:解答题
已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C’,使得∠APF=∠BPC’,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△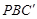 沿
沿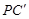 翻折得到△
翻折得到△ ,连接
,连接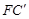 ,取
,取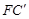 的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.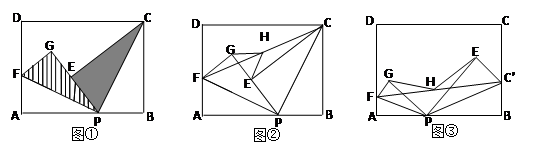
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com