
科目: 来源:2012-2013学年福建武夷山星村中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,四边形ABCD中,∠B=90°,AB=4,BC=3,AD=13,CD=12,求四边形ABCD的面积.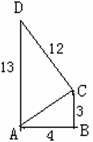
查看答案和解析>>
科目: 来源:2013届广东省深中、宝中、北环中学九年级第三次(5月)模拟数学试卷(带解析) 题型:解答题
如图四边形ABCD是正方形,M是AB延长线上一点。直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F。
(1)如图,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是 ;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ;
③请证明你的上述两猜想;
(2)如图,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想并证明此时DE与EF有怎样的数量关系。
查看答案和解析>>
科目: 来源:2013年浙江省杭州市西湖区中考一模数学试卷(带解析) 题型:解答题
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=DC,点E在对角线BD上,作∠ECF=90°,连接DF,且满足CF=EC.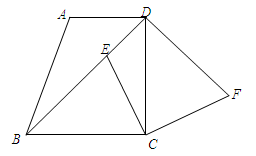
(1)求证:BD⊥DF;
(2)当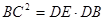 时,试判断四边形DECF的形状,并说明理由.
时,试判断四边形DECF的形状,并说明理由.
查看答案和解析>>
科目: 来源:2012-2013学年江苏省宝应县南片六校七年级下学期5月份调研数学卷(带解析) 题型:解答题
(1)如图,小明画了一个角∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC和BD交与点P,小明通过测量,发现不论怎样变换点A、B的位置,∠APB的度数不发生改变,一直都是130°,请你解释其中的原因。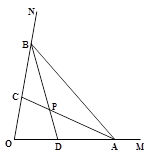
(2)小明想明白后,又开始考虑下图中的问题:△AOB的内角平分线AC和外角平分线BD所构成的∠C是不是也与∠AOB有特数的关系呢?如果∠AOB=n°,那么∠C是多少度呢?请说明理由。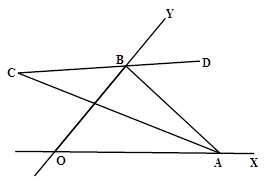
查看答案和解析>>
科目: 来源:2012-2013学年江苏省宝应县南片六校七年级下学期5月份调研数学卷(带解析) 题型:解答题
已知,如图,在直角三角形ABC中,∠ACB=900,D是AB上一点,且∠ACD=∠B
(1)判断△ACD的形状?并说明理由。
(2)你在证明你的结论过程中应用了哪一对互逆的真命题?
查看答案和解析>>
科目: 来源:2012-2013学年浙江台州书生中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,在Rt△ABC中,∠B=90°,BC=6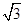 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.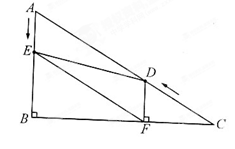
(1)求证:AE=DF.(2分)
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明现由.(5分)
(3)当t为何值时,△DEF为直角三角形?请说明理由.(5分)
查看答案和解析>>
科目: 来源:2012-2013学年江苏省宝应县南片六校八年级下5月月度调研数学卷(带解析) 题型:解答题
如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你在其中选3个作为条件,余下的1个作为结论,使其成为一个真命题,并加以证明。(1)BE=CF,(2)AC = DF,(3)∠ABC=∠DEF,(4)AB=DE.
我所选择的真命题是:
如图,已知:
求证:
证明:
查看答案和解析>>
科目: 来源:2013届福建省福州延安中学九年级中考模拟数学试卷(带解析) 题型:解答题
如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过P点作PF//AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.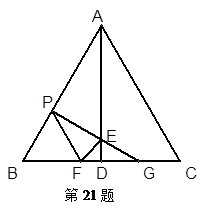
(1)①填空:如果BP=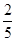 ,则BG= ;
,则BG= ;
②用x的代数式表示线段DG的长,并直接写出自变量x的取值范围;
(2)记△DEF的面积为S,求S与x之间的函数关系式。
(3)当以P、E、F为顶点的三角形与△EDG相似时,请求出BP的长。
查看答案和解析>>
科目: 来源:2013届福建省福州延安中学九年级中考模拟数学试卷(带解析) 题型:解答题
如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD。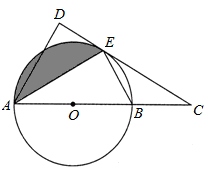
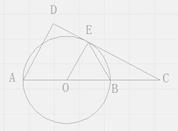
(1)求证:AE平分∠DAC;
(2)若AB=6,∠ABE=60°,①求AD的长;②求出图中阴影部分的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com