
科目: 来源:2012-2013学年湖北省鄂州市第三中学七年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC。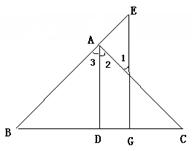
理由如下: AD⊥BC于D,EG⊥BC于G,(已知)
AD⊥BC于D,EG⊥BC于G,(已知) ∠ADC=∠EGC=90°,( )
∠ADC=∠EGC=90°,( ) AD‖EG,( )
AD‖EG,( )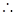 ∠1=∠2,( )
∠1=∠2,( )
=∠3,(两直线平行,同位角相等)
又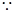 ∠E=∠1(已知)
∠E=∠1(已知)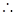 = (等量代换)
= (等量代换) 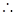 AD平分∠BAC( )
AD平分∠BAC( )
查看答案和解析>>
科目: 来源:2012-2013学年江西省吉安市七校八年级下学期联考数学试卷(带解析) 题型:解答题
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F。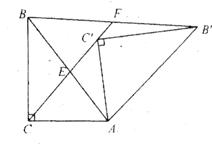
(1)若AC=3,AB=4,求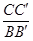
(2)证明:△ACE∽△FBE;
(3)设∠ABC=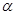 ,∠CAC′=
,∠CAC′=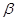 ,试探索
,试探索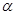 、
、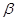 满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。
满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。
查看答案和解析>>
科目: 来源:2012-2013学年江西省吉安市七校八年级下学期联考数学试卷(带解析) 题型:解答题
如图,在12×12的正方形网格中,△TAB的顶点分别为T(1,1),A(2,3),B(4,2)。
(1)以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1的位似中心的同侧将TAB放大为△TA′B′,放大后点A,B的对应点分别为A′,B′,画出△TA′B′,并写出点A′,B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标。
查看答案和解析>>
科目: 来源:2012-2013学年江西省吉安市七校七年级下学期联考数学试卷(带解析) 题型:解答题
如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。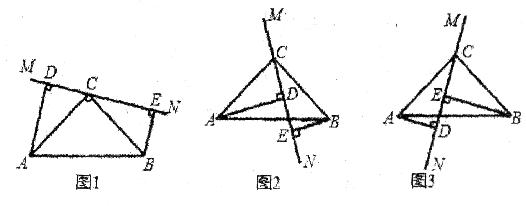
(1)①写出图1中的一对全等三角形;②写出图1中线段DE、AD、BE所具有的等量关系;(不必说明理由)
(2)当直线MN绕点C旋转到图2的位置时,请说明DE=AD-BE的理由;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由)。
查看答案和解析>>
科目: 来源:2012-2013学年江西省吉安市七校七年级下学期联考数学试卷(带解析) 题型:解答题
如图,在四边形ABCD中,∠A=104°,∠ABC=76°,BD⊥CD于点D,EF⊥CD于点F,你能说明∠1=∠2吗?试一试。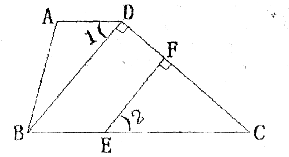
查看答案和解析>>
科目: 来源:2012-2013学年江西省吉安市七校七年级下学期联考数学试卷(带解析) 题型:解答题
如图,已知等腰三角形△ABC,其中AB=AC,∠CAB=40°,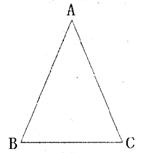
(1)作底角∠ABC的平分线BD,交AC于点D(要求用尺规作图,不用写作法,但要保留作图痕迹)
(2)请计算∠BDC的度数。
查看答案和解析>>
科目: 来源:2013届安徽省毫州市风华中学九年级第四次月考数学试卷(带解析) 题型:解答题
如图,已知∆ABC中,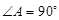 ,
,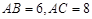 ,D是AB上一动点,DE∥BC,交AC于E,将四边形BDEC沿DE向上翻折,得四边形
,D是AB上一动点,DE∥BC,交AC于E,将四边形BDEC沿DE向上翻折,得四边形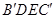 ,
,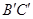 与AB、AC分别交于点M、N.
与AB、AC分别交于点M、N.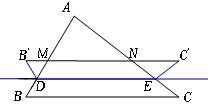
(1)证明:△ADE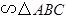 ;
;
(2)设AD为x,梯形MDEN的面积为y,试求y与x的函数关系式. 当x为何值时y有最大值?
查看答案和解析>>
科目: 来源:2012-2013学年安徽省六安地区八年级下期末测试数学试卷(带解析) 题型:解答题
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=4,DC=6,求AD的长. 
小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.
请按照小萍的思路,探究并解答下列问题:
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,证明四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
查看答案和解析>>
科目: 来源:2012-2013学年北京市朝阳区七年级下学期期末考试数学试卷(带解析) 题型:解答题
如图,直线AB、CD交于点A,∠ABC的平分线BD与∠ACB的平分线交于点O,与AC交于点D;过点O作EF//BC交AB于E、交AC于F。若∠BOC=125°,若∠ABC:∠ACB=3:2,求∠AEF和∠EFC的度数。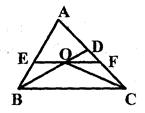
查看答案和解析>>
科目: 来源:2012-2013学年湖北省鄂州市第三中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
[问题情境] 勾股定理是一条古老的数学定理,它有很多证明方法,我国汉代数学家赵爽根据弦图利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”带到其他星球作为地球人与其他星球“人”进行第一次“谈话”的语言。
[定理表述] 请你根据图(1)中的直角三角形叙述勾股定理(用文字及符号语言叙述);

[尝试证明] 以图(1)中的直角三角形为基础可以构造出以a、b为底,以a+b为高的直角梯形如图(2)。请你利用图(2)验证勾股定理;
[知识拓展] 利用图(2)的直角梯形,我们可以证明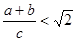 ,其证明步骤如下:
,其证明步骤如下:
∵BC=a+b,AD= .
又∵在直角梯形ABCD中有直角腰BC 斜腰AD(填“>”,“<”或“=”),即 。
∴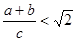
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com