
科目: 来源:2011-2012学年浙江省青田县八年级上学期期末考试数学卷 题型:解答题
(本题6分)如图,四边形ABCD中,AB=BC=2,CD=1,AD=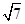 , ∠B=90°.
, ∠B=90°.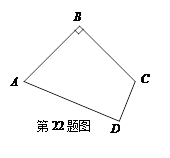
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
查看答案和解析>>
科目: 来源:2012届江苏省南菁中学九年级中考模拟数学试卷2 题型:解答题
提出问题:如图,在“儿童节”前夕,小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕(AD∥BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将自己的这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
背景介绍:这条分割直线既平分了梯形的面积,又平分了梯形的周长,我们称这条线为梯形的“等分积周线”.
【小题1】小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中作出这条“等分积周线”,从而平分蛋糕.

【小题2】小华觉得小明的方法很好,所以模仿着在自己的蛋糕(图2)中画了一条直线EF分别交AD、BC于点E、F.你觉得小华会成功吗?如能成功,说出确定的方法; 如不能成功,请说明理由
如不能成功,请说明理由
【小题3】通过上面的实践,你一定有了更深刻的认识.若图2中AD∥BC,∠A=90°,AD<BC,AB="4" cm,BC ="6" cm,CD= 5cm.请你找出梯形ABCD的所有“等分积周线”,并简要的说明确定的方法.
查看答案和解析>>
科目: 来源:2012届湖北省黄冈市二月份中考摸底考试数学卷 题型:解答题
(7分)已知如图在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥BD交CB的延长线于G.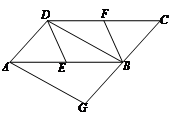
【小题1】(1)求证:△ADE≌△CBF
【小题2】(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论。
查看答案和解析>>
科目: 来源:2012届江苏省启东市东海中学九年级寒假作业检测数学卷 题型:解答题
(本题满分12分)
【小题1】(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,
AB =BC.∴∠NMC=180°—∠AMN—∠
=BC.∴∠NMC=180°—∠AMN—∠ AMB=180°—∠B—∠AMB=∠MAB
AMB=180°—∠B—∠AMB=∠MAB
=∠MAE.
(下面请你完成余下的证明过程)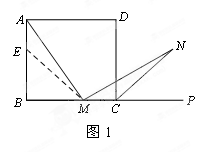
【小题2】(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM= MN是否还成立?请说明理由.
MN是否还成立?请说明理由.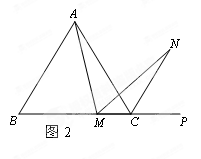
【小题3】(3)若将(1)中的“正方形ABCD”改为“正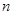 边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
查看答案和解析>>
科目: 来源:2012届北京市第七中学九年级上学期期中检测数学卷 题型:解答题
在△ABC中,BC=a,BC边上的高h=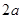 ,沿图中线段DE、CF将△ABC剪开,分成的三块图形恰能拼成正方形CFHG,如图1所示.请你解决如下问题:
,沿图中线段DE、CF将△ABC剪开,分成的三块图形恰能拼成正方形CFHG,如图1所示.请你解决如下问题: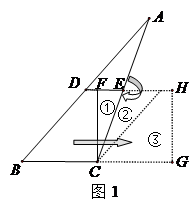
已知:如图2,在△A′B′C′中,B′C′=a,B′C′边上的高h=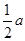 .请你设计两种不同的分割方法,将△A′B′C′沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.
.请你设计两种不同的分割方法,将△A′B′C′沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.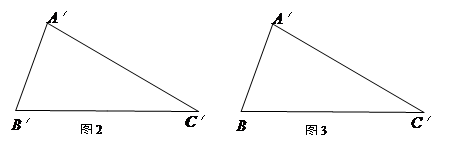
查看答案和解析>>
科目: 来源:2011-2012年宁夏银川芦花中学八年级上学期期末考试数学卷 题型:解答题
(10分)如图,平行四边形ABCD中,EF过AC的中点O,与边AD、BC分别相交于点E、F.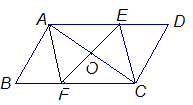
【小题1】(1)试判断四边形AECF的形状,并说明理由.
【小题2】(2)若EF⊥AC,试判断四边形AECF的形状,并说明理由.
【小题3】(3)请添加一个EF与AC满足的条件,使四边形AECF是矩形,并说明理由.
查看答案和解析>>
科目: 来源:2011-2012年宁夏银川芦花中学八年级上学期期末考试数学卷 题型:解答题
(8分)如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=2,且BD=CD,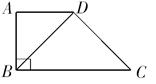
【小题1】(1)求BC的长;
【小题2】(2)求梯形ABCD的面积.
查看答案和解析>>
科目: 来源:2012届北京顺义区中考模拟数学卷 题型:解答题
如图1,矩形纸片ABCD中,AB=4,BC=4 ,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.
,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.
查看答案和解析>>
科目: 来源:2011-2012年北京海淀区九年级第一学期期末考试数学卷 题型:解答题
已知在□ABCD中,AE^BC于E,DF平分ÐADC 交线段AE于F.
【小题1】(1)如图1,若AE=AD,ÐADC=60°, 请直接写出线段CD与AF+BE之间所满足的
等量关系;
【小题2】(2)如图2, 若AE=AD,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论
加以证明, 若不成立, 请说明理由;
【小题3】(3)如图3, 若AE :AD =a :b,试探究线段CD、AF、BE之间所满足的等量关系,请直接写出你的结论.
查看答案和解析>>
科目: 来源:2012届北京通州区中考模拟数学卷 题型:解答题
在图1中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
操作示例
当2b<a时,如图1,在BA上选取点G,使BG=b,连结FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH.
思考发现
小明在操作后发现:该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上.连结CH,由剪拼方法可得DH=BG,故△CHD≌△CGB,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图1),过点F作FM⊥AE于点M(图略),利用SAS公理可判断△HFM≌△CHD,易得FH=HC=GC=FG,∠FHC=90°.进而根据正方形的判定方法,可以判断出四边形FGCH是正方形.
实践探究
【小题1】正方形FGCH的面积是 ;(用含a, b的式子表示)
【小题2】类比图1的剪拼方法,请你就图2—图4的三种情形分别画出剪拼成一个新正方形的示意图.
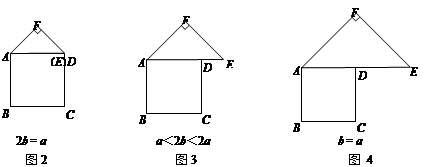
【小题3】联想拓展小明通过探究后发现:当b≤a时,此类图形都能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移.当b>a时(如图5),能否剪拼成一个正方形?若能,请你在图5中画出剪拼成的正方形的示意图;若不能,简要说明理由.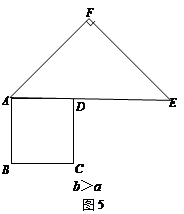
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com