
科目: 来源:2011-2012学年广东省汕头市金平区人教版八年级上册期中考试数学卷 题型:解答题
如图,E是正方形ABCD的边DC上的一点,过点A作FA⊥AE交CB的延长线于点F,求证:DE=BF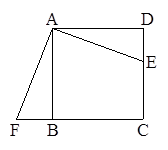
查看答案和解析>>
科目: 来源:2011-2012学年江西省中等学校招生统一考试数学卷(六) 题型:解答题
矩形ABCD中,已知:AD=6,DC=8,矩形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2,连接CF,设AE=x,△FCG的面积=y.
【小题1】如图1,当四边形EFGH为正方形时,求x和y的值;
【小题2】如图2,①求y与x之间的函数关系式与自变量的取值范围;
②连接AC,当EF∥AC时,求x和y的值;
③当△CFG是直角三角形时,求x和y的值.
查看答案和解析>>
科目: 来源:2011-2012学年江西省中等学校招生统一考试数学卷(六) 题型:解答题
如图,已知:在 中,
中, ,
, ,垂足为点
,垂足为点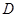 ,
,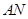 是
是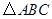 外角
外角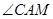 的平分线,
的平分线,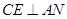 ,垂足为点
,垂足为点 .
.
【小题1】求证:四边形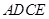 为矩形;
为矩形;
【小题2】当 满足什么条件时,四边形
满足什么条件时,四边形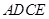 是一个正方形?(不必证明).
是一个正方形?(不必证明).
查看答案和解析>>
科目: 来源:2011-2012学年江西省中等学校招生统一考试数学卷(二) 题型:解答题
课题:探究能拼成正多边形的三角形的面积计算公式.
【小题1】如图1,三角形的三边长分别为a、b、c,∠A=60°,现将六个这样的三角形(设面积为 )拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得
)拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得 = .
= .
【小题2】如图2, 三角形的三边长分别为a、b、c,∠A=120°,试用这样的三角形拼成一个正三角形(设面积为 ),先画出这个正三角形,再推出
),先画出这个正三角形,再推出 的计算公式;
的计算公式;
【小题3】推广:
对于三角形的三边长分别为a、b、c,当∠A取什么值时,能拼成一个任意正 边形吗?如果能,试写出∠A和三角形的面积
边形吗?如果能,试写出∠A和三角形的面积 的表达式;如果不能,请简要说明理由.
的表达式;如果不能,请简要说明理由.
查看答案和解析>>
科目: 来源:2012届江苏省洋思中学九年级下学期第一次月考试数学卷 题型:解答题
(12分)如图,已知矩形ABCD.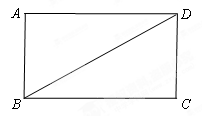
【小题1】(1)在图中作出△CDB沿对角线BD所在直线对折后的△C′DB,C点的对应点为C′(用尺规作图,保留作图痕迹,不要求证明);
【小题2】(2)设C′B与AD的交点为E.
①若DC=3cm,BC=6cm,求△BED的面积;
② 若△BED的面积是矩形ABCD的面积的,求的值.
查看答案和解析>>
科目: 来源:2012届江苏省洋思中学九年级下学期第一次月考试数学卷 题型:解答题
(10分)如图所示,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作BC的平行线交CE的延长线于点F,连接BF.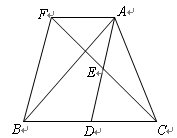
【小题1】(1)求证:AF=BD;
【小题2】(2)如果AB=AC,试证明:四边形AFBD为矩形.
查看答案和解析>>
科目: 来源:2012届陕西省兴平市秦岭中学九年级上学期期末练习数学卷 题型:解答题
(本题满分12分)
已知菱形ABCD的边长为1.∠ADC=60°,等边△AEF两边分别交边DC、CB于点E、F。
【小题1】(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为等边△AEF的外心;
【小题2】(2)若点E、F始终分别在边DC、CB上移动.记等边△AEF的外心为点P.
①猜想验证:如图2.猜想△AEF的外心P落在哪一直线上,并加以证明;
②拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,试判断 是否为定值.若是.请求出该定值;若不是.请说明理由。
是否为定值.若是.请求出该定值;若不是.请说明理由。
查看答案和解析>>
科目: 来源:2011-2012学年福建省漳州市八年级上学期期末考试数学卷 题型:解答题
(本题8分)如图,在梯形ABCD中,AB∥DC,AB=14cm,CD=6cm.点P从点A出发,以2cm/s的速度沿AB向终点B运动;点Q从点C出发,以1cm/s的速度沿CD向终点D运动(P、Q两点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒。
(1)当DQ=AP时,四边形APQD是平形四边形,求出此时t的值;
(2) 试问在这样的运动过程中,是否存在某一时刻,使梯形PBCQ的面积是梯形ABCD面积的一半?若存在,求出这样的t的值,若不存在,请说明理由。
 |
查看答案和解析>>
科目: 来源:2011-2012学年福建省漳州市八年级上学期期末考试数学卷 题型:解答题
(本题6分)如图,在平行四边形ABCD中,点E是BC边上的一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=56°求∠D的度数.
解: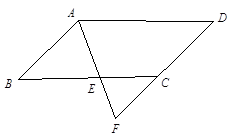
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com