
科目: 来源:2012届湖北黄石九年级5月联考数学试卷(带解析) 题型:解答题
如图1,将正方形纸片 折叠,使点
折叠,使点 落在
落在 边上一点
边上一点 (不与点
(不与点 ,
, 重合),压平后得到折痕
重合),压平后得到折痕 .
.
【小题1】当 时,求
时,求 的值.(方法指导:为了求得
的值.(方法指导:为了求得 的值,可先求
的值,可先求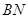 、
、 的长,不妨设
的长,不妨设 =2)
=2)
【小题2】在图1中,若 则
则 的值等于 ;若
的值等于 ;若 则
则 的值等于 ;若
的值等于 ;若 (
( 为整数),则
为整数),则 的值等于 .(用含
的值等于 .(用含 的式子表示)
的式子表示)
【小题3】如图2,将矩形纸片 折叠,使点
折叠,使点 落在
落在 边上一点
边上一点 (不与点
(不与点 重合),压平后得到折痕
重合),压平后得到折痕 设
设 则
则 的值等于 .(用含
的值等于 .(用含 的式子表示)
的式子表示)
查看答案和解析>>
科目: 来源:2011-2012学年山东胜利七中八年级上学期期末数学试卷(带解析) 题型:解答题
已知:如图,在直角梯形ABCD中,AD // BC,AB⊥AD,BC = CD,BE⊥CD,垂足为点E,点F在BD上,联结AF、EF.
【小题1】求证:AD = ED;
【小题2】如果AF // CD,求证:四边形ADEF是菱形
查看答案和解析>>
科目: 来源:2011-2012学年河南师大附中八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,E、F,是平行四边形ABCD的对角线AC上的两点,AF=CE连接D,E,F和F,B.求证:四边形DFBE是平行四边形。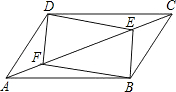
查看答案和解析>>
科目: 来源:2011-2012学年江苏启东东海中学八年级下学期第二次学情调研数学试卷 题型:解答题
如图,在梯形 中,
中, 两点在边
两点在边 上,且四边形
上,且四边形 是平行四边形.
是平行四边形.
【小题1】 与
与 有何等量关系?请说明理由
有何等量关系?请说明理由
【小题2】当 时,求证:四边形
时,求证:四边形 是矩形
是矩形
查看答案和解析>>
科目: 来源:2011-2012学年江苏省姜堰市四校七年级下学期月度联考数学卷(带解析) 题型:解答题
(12分)如图,△ABC和△ADC都是边长相等的等边三角形,点E、F同时分别从点B、 A出发,各自沿BA、AD方向运动到点A、D停止,运动的速度相同,连接EC、FC.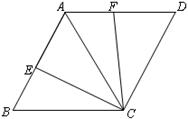
(1)写出在点E、F运动过程中,所有全等的三角形。
(2)点E、F运动过程中∠ECF的大小是否随之变化?请说明理由;
(3)点E、F运动过程中,以点A、E、C、F为顶点的四边形的面积变化吗?请说明理由;
(4)接EF,在图中找出和∠ACE相等的所有角,并说明理由.
查看答案和解析>>
科目: 来源:2012届广东省汕头市濠江区中考模拟考试数学卷(带解析) 题型:解答题
如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?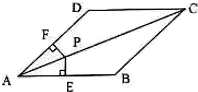
查看答案和解析>>
科目: 来源:2011届江苏南京市第三初级中学九年级上学期期中考试数学卷(带解析) 题型:解答题
如图,将边长为3cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD的中点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
(1) △AEM的周长=_____cm;(2)求证:EP=AE+DP;
查看答案和解析>>
科目: 来源:2011届江苏南京市第三初级中学九年级上学期期中考试数学卷(带解析) 题型:解答题
已知:如图,△ABC中,AD是BC边上的中线,四边形ABDE是平行四边形
(1)求证:四边形ADCE是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCE是菱形?说明你的理由.
查看答案和解析>>
科目: 来源:2011届江苏南京市第三初级中学九年级下学期10月月考数学卷(带解析) 题型:解答题
已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.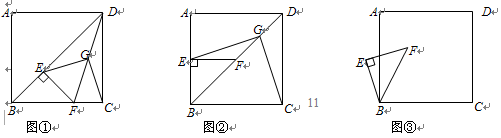
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45º,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
查看答案和解析>>
科目: 来源:2011届江苏南京市第三初级中学九年级下学期10月月考数学卷(带解析) 题型:解答题
如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正 边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.
边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.
(直接写出答案,不需要证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com